题目内容
(理)斜率为1的直线过抛物线y2=2px(p>0)的焦点,且与抛物线交于两点A、B.(1)若p=2,求|AB|的值;
(2)将直线AB按向量
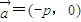 平移得直线m,N是m上的动点,求
平移得直线m,N是m上的动点,求 的最小值.
的最小值.(3)设C(p,0),D为抛物线y2=2px(p>0)上一动点,是否存在直线l,使得l被以CD为直径的圆截得的弦长恒为定值?若存在,求出l的方程;若不存在,说明理由.
【答案】分析:(1)由已知条件,得到抛物线的方程,再根据抛物线的定义得到|AB|=x1+x2+p=4p,
(2)设直线l的方程,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量坐标运算,求得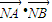 的以N点坐标表示的函数式,利用二次函数求最值的方法,可求得所求的最小值.
的以N点坐标表示的函数式,利用二次函数求最值的方法,可求得所求的最小值.
(3)对于存在性问题,可先假设存在,即假设满足条件的直线l存在,其方程为x=a,再利用l被以CD为直径的圆截得的弦长恒为定值,求出p,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)设A(x1,y1),B(x2,y2),p=2时,直线AB:y=x-1,代入y2=4x中
可得:x2-6x+1=0(2分)
则x1+x2=6,由定义可得:|AB|=x1+x2+p=8.(4分)
(2)直线AB: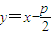 ,代入y2=2px(p>0)中,可得:
,代入y2=2px(p>0)中,可得: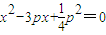
则x1+x2=3p,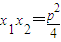 ,设
,设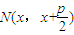 ,
,
则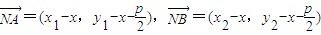
即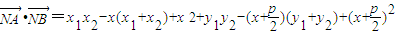 (2分)
(2分)
由 (4分)
(4分)
则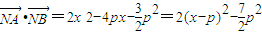
当x=p时,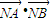 的最小值为
的最小值为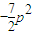 . (6分)
. (6分)
(3)假设满足条件的直线l存在,其方程为x=a,
设CD的中点为O',l与以CD为直径的圆相交于点P、Q,设PQ的中点为H,
则O'H⊥PQ,O'点的坐标为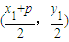 .
.
∵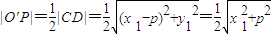 ,
,
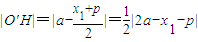 ,(2分)
,(2分)
∴|PH|2=|O'P|2-|O'H|2=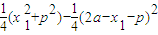 =
=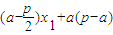 ,
,
∴|PQ|2=(2|PH|)2=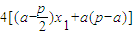 . (5分)
. (5分)
令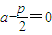 ,得
,得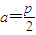 ,此时|PQ|=p为定值,
,此时|PQ|=p为定值,
故满足条件的直线l存在,其方程为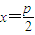 ,即抛物线的通径所在的直线. (7分)
,即抛物线的通径所在的直线. (7分)
点评:此题考查抛物线的定义,及向量坐标运算等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
(2)设直线l的方程,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用向量坐标运算,求得
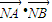 的以N点坐标表示的函数式,利用二次函数求最值的方法,可求得所求的最小值.
的以N点坐标表示的函数式,利用二次函数求最值的方法,可求得所求的最小值.(3)对于存在性问题,可先假设存在,即假设满足条件的直线l存在,其方程为x=a,再利用l被以CD为直径的圆截得的弦长恒为定值,求出p,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:解:(1)设A(x1,y1),B(x2,y2),p=2时,直线AB:y=x-1,代入y2=4x中
可得:x2-6x+1=0(2分)
则x1+x2=6,由定义可得:|AB|=x1+x2+p=8.(4分)
(2)直线AB:
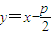 ,代入y2=2px(p>0)中,可得:
,代入y2=2px(p>0)中,可得: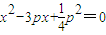
则x1+x2=3p,
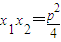 ,设
,设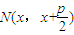 ,
,则
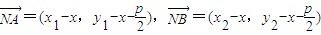
即
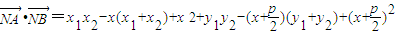 (2分)
(2分)由
 (4分)
(4分)则
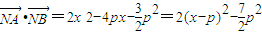
当x=p时,
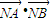 的最小值为
的最小值为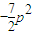 . (6分)
. (6分)(3)假设满足条件的直线l存在,其方程为x=a,
设CD的中点为O',l与以CD为直径的圆相交于点P、Q,设PQ的中点为H,
则O'H⊥PQ,O'点的坐标为
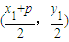 .
.∵
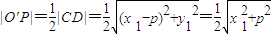 ,
,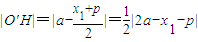 ,(2分)
,(2分)∴|PH|2=|O'P|2-|O'H|2=
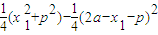 =
=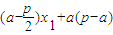 ,
,∴|PQ|2=(2|PH|)2=
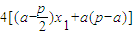 . (5分)
. (5分)令
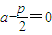 ,得
,得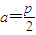 ,此时|PQ|=p为定值,
,此时|PQ|=p为定值,故满足条件的直线l存在,其方程为
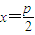 ,即抛物线的通径所在的直线. (7分)
,即抛物线的通径所在的直线. (7分)点评:此题考查抛物线的定义,及向量坐标运算等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
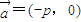 平移得直线m,N是m上的动点,求
平移得直线m,N是m上的动点,求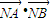 的最小值.
的最小值.