题目内容
已知圆M:(x-m)2+(y-n)2=4(m,n∈R),圆M与y轴交于A,B两点,若|
+
|=2,则|
=
| MA |
| MB |
| AB| |
2
| 3 |
2
.| 3 |
分析:设AB的中点为C,连结CM,利用平面向量的加法法则和垂径定理,结合题中数据在Rt△ACM中算出AC长,即可得到向量
的模.
| AB |
解答:解: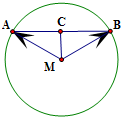 设AB的中点为C,连结CM,
设AB的中点为C,连结CM,
由平面向量的加法法则,可得
+
=2
∵|
+
|=2,∴
=1
∵AB是圆M的弦,C为AB中点,∴CM⊥AB,
由圆的方程得圆半径为2,
Rt△ACM中,|
|=
=
=
,可得|
|=2|
|=2
.
故答案为:2
 设AB的中点为C,连结CM,
设AB的中点为C,连结CM,由平面向量的加法法则,可得
| MA |
| MB |
| MC |
∵|
| MA |
| MB |
| |MC| |
∵AB是圆M的弦,C为AB中点,∴CM⊥AB,
由圆的方程得圆半径为2,
Rt△ACM中,|
| AC |
|
| 22-12 |
| 3 |
| AB |
| AC |
| 3 |
故答案为:2
| 3 |
点评:本题给出圆的弦AB满足的向量式,求弦AB的长.着重考查了圆的性质、平面向量的加法法则和勾股定理等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
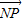 =2
=2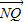 ,
, •
•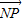 =0.
=0.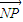 =2
=2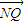 ,
,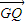 •
•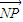 =0.
=0.