题目内容
已知圆M:(x-m)
2+(y-n)
2=γ
2及定点N(1,0),点P是圆M上的动点,点Q在NP上,点G在MP上,且满足
=2
,
•
=0.
(Ⅰ)若m=-1,n=0,r=4,求点G的轨迹C的方程;
(Ⅱ)若动圆M和(Ⅰ)中所求轨迹C相交于不同两点A、B,是否存在一组正实数m,n,r使得直线MN垂直平分线段AB,若存在,求出这组正实数;若不存在,说明理由.
分析:(Ⅰ)先利用向量间的关系求出点Q为PN的中点以及|PG|=|GN|,可得点G的轨迹是以M,N为焦点的椭圆进而求出点G的轨迹C的方程;
(Ⅱ)先假设存在,利用点差法(把点的坐标代入椭圆后两方程作差)求出直线的斜率和中点坐标之间的关系,再利用直线MN垂直平分线段AB求出中点横坐标,与条件相比较可得结论.
解答:解:(Ⅰ)∵
=2,
∴点Q为PN的中点,
又∵
•=0,
∴GQ⊥PN或G点与Q点重合.
∴|PG|=|GN|.(2分)
又|GM|+|GN|=|GM|+|GP|=|PM|=4.
∴点G的轨迹是以M,N为焦点的椭圆,且a=2,c=1.
∴
b==,∴G的轨迹方程是
+=1.(5分)
(Ⅱ)解:不存在这样一组正实数,下面证明:(6分)
由题意,若存在这样的一组正实数,当直线MN的斜率存在时,设之为k,
故直线MN的方程为:y=k(x-1),
设A(x
1,y
1),B(x
2,y
2),AB中点D(x
0,y
0),
则
,
两式相减得:
+=0,①(8分)
注意到
=-,且
,
则
=.②
又点D在直线MN上,
∴y
0=k(x
0-1),代入②式得:x
0=4,
因为弦AB的中点D在(1)所给椭圆C内,
故-2<x
0<2,这与x
0=4矛盾.
所以所求这组正实数不存在.(11分)
当直线MN的斜率不存在时,直线MN的方程为x=1,
则此时y
1=y
2,x
1+x
2=2,
代入①式得x
1-x
2=0,这与A,B是不同两点矛盾.
综上,所求的这组正实数不存在.(12分)
点评:本题是对圆,椭圆,向量以及直线与圆锥曲线位置关系的综合考查,由于知识点较多,是道难题.
练习册系列答案
相关题目

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案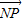 =2
=2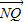 ,
, •
•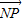 =0.
=0.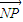 =2
=2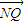 ,
,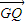 •
•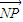 =0.
=0.