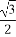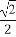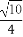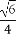题目内容

下列命题中正确的个数是(　　)

①若直线a不在α内,则a∥α;

②若直线l上有无数个点不在平面α内,则l∥α;

③若l与平面α平行,则l与α内任何一条直线都没有公共点;

④平行于同一平面的两直线可以相交.

(A)1 (B)2 (C)3 (D)4

 

B

【解析】a∩α=A时,a?α,∴①错;

直线l与α相交时,l上有无数个点不在α内,故②错;

l∥α,l与α无公共点,∴l与α内任一直线都无公共点,③正确;长方体中A1C1与B1D1都与平面ABCD平行,∴④正确.

 

练习册系列答案
相关题目

已知集合A={x|x2-2x-3>0},B={x|x2+ax+b≤0},若A∪B=R,A∩B={x|3<x≤4},则a+b的值等于　　　.

 

设α,β表示两个不同平面,l,m表示两条不同的直线,则下列命题正确的是(　　)

(A)若l⊥m,l?α,m?β,则α⊥β

(B)若l⊥α,m∥β,α⊥β,则l⊥m

(C)若l∥m,l?α,m⊥β,则α∥β

(D)若l⊥α,m⊥β,α∥β,则l∥m

 

已知向量a=(2,-3,5)与向量b=(3,λ,)平行,则λ=(　　)

(A) (B) (C)- (D)-

 

设互不相同的直线l,m,n和平面α,β,γ,给出下列三个命题:

①若l与m为异面直线,l?α,m?β,则α∥β;

②若α∥β,l?α,m?β,则l∥m;

③若α∩β=l,β∩γ=m,γ∩α=n,l∥γ,则m∥n.

其中真命题的个数为　　　　.

 

正三棱柱(底面为正三角形的直棱柱)ABC-A1B1C1如图所示,以四边形ABB1A1为水平面,四边形BCC1B1的前面为正前方画出的三视图正确的是( )

 

 

一个正方体截去两个角后所得几何体的正视图(又称主视图)、侧视图(又称左视图)如图所示,则其俯视图为( )

 

 

在三棱柱ABC-A1B1C1中,底面为边长为1的正三角形,侧棱AA1⊥底面ABC,点D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则sinα的值为(　　)

(A) (B) (C) (D)

 

若数列{an}的通项公式an=,记cn=2(1-a1)·(1-a2)…(1-an),试通过计算c1,c2,c3的值,推测cn=　　　.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网