题目内容
在区间(0,2)内任取两数m,n(m≠n),则椭圆
+
=1的离心率大于
的概率是______.
| x2 |
| m2 |
| y2 |
| n2 |
| ||
| 2 |
区间(0,2)内任取两个实数计为(m,n),
则点对应的平面区域为下图所示的正方形,
当m>n时,椭圆
+
=1的离心率e=
>
,化简得,m>2n;
当M<n时,椭圆
+
=1的离心率e=
>
,化简得,n>2m;
故其中满足椭圆
+
=1的离心率大于
时,有m>2n或n>2m.
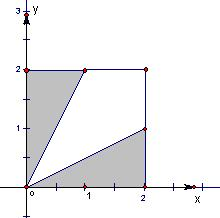
它表示的平面区域如下图中阴影部分所示:
其中正方形面积S=4,阴影部分面积S阴影=2×
×2×1=2.
∴所求的概率P=
=
故答案为:
.
则点对应的平面区域为下图所示的正方形,
当m>n时,椭圆
| x2 |
| m2 |
| y2 |
| n2 |
| ||
| m |
| ||
| 2 |
当M<n时,椭圆
| x2 |
| m2 |
| y2 |
| n2 |
| ||
| n |
| ||
| 2 |
故其中满足椭圆
| x2 |
| m2 |
| y2 |
| n2 |
| ||
| 2 |
它表示的平面区域如下图中阴影部分所示:
其中正方形面积S=4,阴影部分面积S阴影=2×
| 1 |
| 2 |
∴所求的概率P=
| S阴影 |
| S |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |


练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目


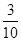
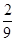
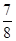
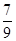
 颗蓝骰子,观察向上的点数,记“红骰子向上的点数是3的倍数”为事件
颗蓝骰子,观察向上的点数,记“红骰子向上的点数是3的倍数”为事件