题目内容
已知方程：（m-1）x2+（3-m）y2=（m-1）（3-m）表示焦距为8的双曲线，则m的值等于
- A.-30
- B.10
- C.-6或10
- D.-30或34
C
分析：将方程化简，再分类讨论，确定几何量，利用焦距为8，即可求得结论．
解答：方程：（m-1）x2+（3-m）y2=（m-1）（3-m）可化为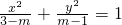
当焦点在x轴上时，a2=3-m，b2=1-m，c2=a2+b2=4-2m，∴4-2m=16，∴m=-6；
当焦点在y轴上时，a2=m-1，b2=m-3，c2=a2+b2=2m-4，∴2m-4=16，∴m=10
综上知，m的值等于-6或10
故选C．
点评：本题考查双曲线的几何性质，考查学生的计算能力，考查分类讨论的数学思想，属于基础题．
分析：将方程化简，再分类讨论，确定几何量，利用焦距为8，即可求得结论．
解答：方程：（m-1）x2+（3-m）y2=（m-1）（3-m）可化为
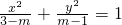
当焦点在x轴上时，a2=3-m，b2=1-m，c2=a2+b2=4-2m，∴4-2m=16，∴m=-6；
当焦点在y轴上时，a2=m-1，b2=m-3，c2=a2+b2=2m-4，∴2m-4=16，∴m=10
综上知，m的值等于-6或10
故选C．
点评：本题考查双曲线的几何性质，考查学生的计算能力，考查分类讨论的数学思想，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
已知方程
+
=1表示焦点在x轴上的椭圆，则m的取值范围是（ ）
| x2 |
| m2 |
| y2 |
| 2+m |
| A、m＞2或m＜-1 |
| B、m＞-2 |
| C、-1＜m＜2 |
| D、m＞2或-2＜m＜-1 |