题目内容
已知方程cosx-sinx=m-1无实数解,则实数m的取值范围分析:利用两角和的正弦函数化简方程cosx-sinx=m-1为:
cos( x+
)=am-1解集是空集,就是m不在[-
+1,
+1]区间内,求出即可.
| 2 |
| π |
| 4 |
| 2 |
| 2 |
解答:解:方程化简为:
cos( x+
)=m-1,
即 cos( x+
)=
若没有解集,那么
>1或
<-1
解得 m>
+1或m<-
+1;
故答案为:(-∞,-
+1)∪(
+1,+∞).
| 2 |
| π |
| 4 |
即 cos( x+
| π |
| 4 |
| ||
| 2 |
若没有解集,那么
| ||
| 2 |
| ||
| 2 |
解得 m>
| 2 |
| 2 |
故答案为:(-∞,-
| 2 |
| 2 |
点评:本题考查三角函数的最值,空集的概念,考查计算能力,解题的关键是:m不在[-
+1,
+1]区间内.是基础题.
| 2 |
| 2 |

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 ]上的函数y=f(x)的图象关于直线x=
]上的函数y=f(x)的图象关于直线x= 对称,当x
对称,当x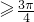 时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为
时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为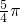


 ]上的函数y=f(x)的图象关于直线x=
]上的函数y=f(x)的图象关于直线x= 对称,当x
对称,当x 时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )
时,f(x)=cosx,如果关于x的方程f(x)=a有解,记所有解的和为S,则S不可能为( )

