题目内容
已知椭圆 的右焦点与抛物线
的右焦点与抛物线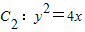 的焦点F重合,椭圆C1与抛物线C2在第一象限的交点为P,
的焦点F重合,椭圆C1与抛物线C2在第一象限的交点为P,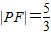 .
.(1)求椭圆C1的方程;
(2)若过点A(-1,0)的直线与椭圆C1相交于M、N两点,求使
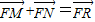 成立的动点R的轨迹方程;
成立的动点R的轨迹方程;(3)若点R满足条件(2),点T是圆(x-1)2+y2=1上的动点,求|RT|的最大值.
【答案】分析:(1)抛物线y2=4x的焦点F的坐标为(1,0),准线为x=-1,设点P的坐标为(x,y),依据抛物线的定义,由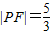 ,可求x.由点P在抛物线C2上,且在第一象限可求点P的坐标,再由点P在椭圆上及c=1,a2=b2+c2=b2+1,可求a,b,从而可求椭圆的方程
,可求x.由点P在抛物线C2上,且在第一象限可求点P的坐标,再由点P在椭圆上及c=1,a2=b2+c2=b2+1,可求a,b,从而可求椭圆的方程
(2)设点M(x1,y1)、N(x2,y2)、R(x,y),则由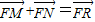 ,可得x1+x2-2=x-1,y1+y2=y.利用设而不求的方法可得
,可得x1+x2-2=x-1,y1+y2=y.利用设而不求的方法可得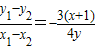 设FR的中点为Q,由M、N、Q、A四点共线可得
设FR的中点为Q,由M、N、Q、A四点共线可得 =
=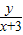 ,从而可得动点R的轨迹方程;
,从而可得动点R的轨迹方程;
(3)确定椭圆的左顶点,圆与x轴的交点坐标,即可求|RT|的最大值.
解答:解:(1)抛物线C2:y2=4x的焦点F的坐标为(1,0),准线为x=-1,
设点P的坐标为(x,y),依据抛物线的定义,由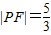 ,得1+x=
,得1+x= ,解得x=
,解得x= .
.
∵点P在抛物线C2上,且在第一象限,∴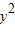 =4x=4×
=4x=4× ,解得y=
,解得y=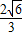 .
.
∴点P的坐标为( ,
,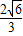 ).
).
∵点P在椭圆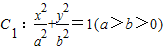 上,∴
上,∴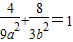 .
.
又c=1,且a2=b2+c2=b2+1,解得a2=4,b2=3.
∴椭圆C1的方程为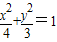 .
.
(2)设点M(x1,y1)、N(x2,y2)、R(x,y),
则 =(x1-1,y1),
=(x1-1,y1),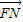 =(x2-1,y2),
=(x2-1,y2),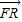 =(x-1,y).
=(x-1,y).
∴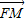 +
+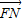 =(x1+x2-2,y1+y2).
=(x1+x2-2,y1+y2).
∵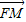 +
+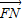 =
=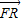 ,
,
∴x1+x2-2=x-1,y1+y2=y.①
∵M、N在椭圆C1上,∴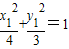 ,
,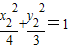 .
.
上面两式相减,把①式代入得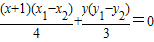 .
.
当x1≠x2时,得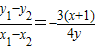 .②
.②
设FR的中点为Q,则Q的坐标为(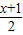 ,
,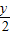 ).
).
∵M、N、Q、A四点共线,∴kMN=kAQ,即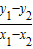 =
=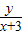 .③
.③
把③式代入②式,得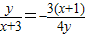 ,化简得4y2+3(x2+4x+3)=0.
,化简得4y2+3(x2+4x+3)=0.
当x1=x2时,可得点R的坐标为(-3,0),
经检验,点R(-3,0)在曲线4y2+3(x2+4x+3)=0上.
∴动点R的轨迹方程为4y2+3(x2+4x+3)=0.
(3)4y2+3(x2+4x+3)=0可化为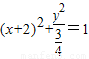 ,中心为(-2,0),焦点在x轴上,左顶点坐标为(-3,0)
,中心为(-2,0),焦点在x轴上,左顶点坐标为(-3,0)
∵圆(x-1)2+y2=1的圆心坐标为(1,0),与x轴的交点坐标为(0,0),(2,0)
∴|RT|的最大值为2-(-3)=5.
点评:圆锥曲线的性质与圆锥曲线的定义相结合,在解题时要注意灵活应用这样可以简化运算在直线与椭圆的位置关系中涉及到直线的斜率、线段的中点结合在一起的问题,“设而不求”得做法可以简化解题的基本运算,这是解决此类问题的重要方法.
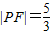 ,可求x.由点P在抛物线C2上,且在第一象限可求点P的坐标,再由点P在椭圆上及c=1,a2=b2+c2=b2+1,可求a,b,从而可求椭圆的方程
,可求x.由点P在抛物线C2上,且在第一象限可求点P的坐标,再由点P在椭圆上及c=1,a2=b2+c2=b2+1,可求a,b,从而可求椭圆的方程(2)设点M(x1,y1)、N(x2,y2)、R(x,y),则由
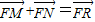 ,可得x1+x2-2=x-1,y1+y2=y.利用设而不求的方法可得
,可得x1+x2-2=x-1,y1+y2=y.利用设而不求的方法可得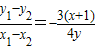 设FR的中点为Q,由M、N、Q、A四点共线可得
设FR的中点为Q,由M、N、Q、A四点共线可得 =
=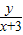 ,从而可得动点R的轨迹方程;
,从而可得动点R的轨迹方程;(3)确定椭圆的左顶点,圆与x轴的交点坐标,即可求|RT|的最大值.
解答:解:(1)抛物线C2:y2=4x的焦点F的坐标为(1,0),准线为x=-1,
设点P的坐标为(x,y),依据抛物线的定义,由
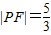 ,得1+x=
,得1+x= ,解得x=
,解得x= .
.∵点P在抛物线C2上,且在第一象限,∴
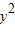 =4x=4×
=4x=4× ,解得y=
,解得y=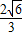 .
.∴点P的坐标为(
 ,
,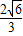 ).
).∵点P在椭圆
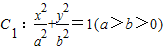 上,∴
上,∴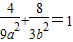 .
.又c=1,且a2=b2+c2=b2+1,解得a2=4,b2=3.
∴椭圆C1的方程为
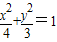 .
.(2)设点M(x1,y1)、N(x2,y2)、R(x,y),
则
 =(x1-1,y1),
=(x1-1,y1),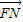 =(x2-1,y2),
=(x2-1,y2),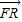 =(x-1,y).
=(x-1,y).∴
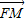 +
+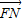 =(x1+x2-2,y1+y2).
=(x1+x2-2,y1+y2).∵
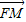 +
+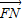 =
=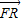 ,
,∴x1+x2-2=x-1,y1+y2=y.①
∵M、N在椭圆C1上,∴
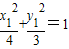 ,
,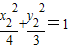 .
.上面两式相减,把①式代入得
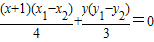 .
.当x1≠x2时,得
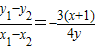 .②
.②设FR的中点为Q,则Q的坐标为(
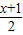 ,
,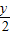 ).
).∵M、N、Q、A四点共线,∴kMN=kAQ,即
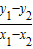 =
=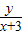 .③
.③把③式代入②式,得
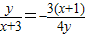 ,化简得4y2+3(x2+4x+3)=0.
,化简得4y2+3(x2+4x+3)=0.当x1=x2时,可得点R的坐标为(-3,0),
经检验,点R(-3,0)在曲线4y2+3(x2+4x+3)=0上.
∴动点R的轨迹方程为4y2+3(x2+4x+3)=0.
(3)4y2+3(x2+4x+3)=0可化为
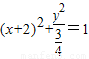 ,中心为(-2,0),焦点在x轴上,左顶点坐标为(-3,0)
,中心为(-2,0),焦点在x轴上,左顶点坐标为(-3,0)∵圆(x-1)2+y2=1的圆心坐标为(1,0),与x轴的交点坐标为(0,0),(2,0)
∴|RT|的最大值为2-(-3)=5.
点评:圆锥曲线的性质与圆锥曲线的定义相结合,在解题时要注意灵活应用这样可以简化运算在直线与椭圆的位置关系中涉及到直线的斜率、线段的中点结合在一起的问题,“设而不求”得做法可以简化解题的基本运算,这是解决此类问题的重要方法.

练习册系列答案
相关题目
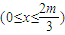 和椭圆弧
和椭圆弧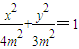

 和椭圆弧
和椭圆弧
