题目内容
(本题满分18分)第一题满分4分,第二题满分6分,第三题满分8分.
已知椭圆![]() 的长轴长是焦距的两倍,其左、右焦点依次为
的长轴长是焦距的两倍,其左、右焦点依次为![]() 、
、![]() ,抛物线
,抛物线![]()
![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,椭圆
,椭圆![]() 与抛物线
与抛物线![]() 的一个交点为
的一个交点为![]() .
.
(1)当![]() 时,求椭圆
时,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下,直线![]() 过焦点
过焦点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点,若弦长
两点,若弦长![]() 等于
等于![]() 的周长,求直线
的周长,求直线![]() 的方程;
的方程;
(3)由抛物线弧![]()
![]() 和椭圆弧
和椭圆弧![]()
![]()
(![]() )合成的曲线叫“抛椭圆”,是否存在以原点
)合成的曲线叫“抛椭圆”,是否存在以原点![]() 为直角顶点,另两个顶点
为直角顶点,另两个顶点![]() 落在“抛椭圆”上的等腰直角三角形
落在“抛椭圆”上的等腰直角三角形![]() ,若存在,求出两直角边所在直线的斜率;若不存在,说明理由.
,若存在,求出两直角边所在直线的斜率;若不存在,说明理由.
解:(1)设椭圆的实半轴长为a,短半轴长为b,半焦距为c,
当![]() =1时,由题意得,a=2c=2,
=1时,由题意得,a=2c=2,![]() ,
,
所以椭圆的方程为![]() .(4分)
.(4分)
(2)依题意知直线![]() 的斜率存在,设
的斜率存在,设![]() ,由
,由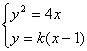 得,
得,![]() ,由直线
,由直线![]() 与抛物线
与抛物线![]() 有两个交点,可知
有两个交点,可知![]() .设
.设![]() ,由韦达定理得
,由韦达定理得![]() ,则
,则![]() (6分)又
(6分)又![]() 的周长为
的周长为![]() ,所以
,所以![]() , (8分)
, (8分)
解得![]() ,从而可得直线
,从而可得直线![]() 的方程为
的方程为![]() (10分)
(10分)
(3)由题意得,“抛椭圆”由抛物线弧![]() 和椭圆弧
和椭圆弧![]() 合成,且
合成,且![]() 、
、![]() 。
。
假设存在![]()
![]() 为等腰直角三角形,由
为等腰直角三角形,由![]() 所在曲线的位置做如下3种情况讨论:
所在曲线的位置做如下3种情况讨论:
①当![]() 同时在抛物线弧
同时在抛物线弧![]() 上时,由
上时,由![]() 、
、![]() 的斜率分别为
的斜率分别为![]() ,
,![]() 比为钝角,显然与题设矛盾. 此时不存在 (12分)
比为钝角,显然与题设矛盾. 此时不存在 (12分)
② 当![]() 同时在椭圆弧
同时在椭圆弧![]() 上时,由椭圆与等腰直角三角形的对称性知,则两直角边关于x轴对称.即直线
上时,由椭圆与等腰直角三角形的对称性知,则两直角边关于x轴对称.即直线![]() 的斜率为1,直线
的斜率为1,直线![]() 的斜率为
的斜率为![]() ,
,
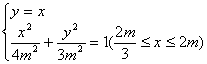 得
得![]()
![]() 符合题意;此时存在(15分)
符合题意;此时存在(15分)
③ 不妨设当![]() 在抛物线弧上,
在抛物线弧上,![]() 在椭圆弧上时,
在椭圆弧上时,
于是设直线![]() 的方程为
的方程为![]() (其中
(其中![]() ),将其代入
),将其代入![]()
![]() 得
得![]() ;由
;由![]() ,直线
,直线![]() 的方程为
的方程为![]() ,同理代入椭圆弧方程
,同理代入椭圆弧方程![]()
![]() 得
得![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() 与
与![]() 矛盾,此时不存在。
矛盾,此时不存在。
因此,存在以原点![]() 为直角顶点,另两个顶点
为直角顶点,另两个顶点![]() 落在“抛椭圆”上的等腰直角三角形
落在“抛椭圆”上的等腰直角三角形![]() ,两直角边所在直线的斜率分别为1和
,两直角边所在直线的斜率分别为1和![]() .(18分)
.(18分)

练习册系列答案
相关题目
 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当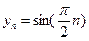 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
( 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
. ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
( ,
,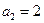 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,如果存在一个正整数
,如果存在一个正整数 ,使得对任意的
,使得对任意的 (
( )都有
)都有 成立,那么就把这样一类数列
成立,那么就把这样一类数列 时
时 的周期数列,当
的周期数列,当 时
时 是周期为
是周期为 的周期数列。
的周期数列。 满足
满足 (
( (
(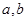 不同时为0),且数列
不同时为0),且数列 的周期数列,求常数
的周期数列,求常数 的值;
的值; ,且
,且 .
.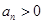 ,试判断数列
,试判断数列 ,试判断数列
,试判断数列 (
(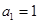 ,
,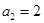 ,
, ,数列
,数列 的前
的前 ,使对任意的
,使对任意的 成立,若存在,求出
成立,若存在,求出 ,其中
,其中 .
. 时,设
时,设 ,
, ,求
,求 的解析式及定义域;
的解析式及定义域; 时,求
时,求 的最小值;
的最小值; ,当
,当 时,
时, 对任意
对任意 恒成立,求
恒成立,求 的取值范围.
的取值范围. 是等差数列,且公差为
是等差数列,且公差为 ,若数列
,若数列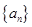 中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”.
中任意(不同)两项之和仍是该数列中的一项,则称该数列是“封闭数列”. ,求证:该数列是“封闭数列”;
,求证:该数列是“封闭数列”; 是否是“封闭数列”,为什么?
是否是“封闭数列”,为什么? 是数列
是数列 项和,若公差
项和,若公差 ,试问:是否存在这样的“封闭数列”,使
,试问:是否存在这样的“封闭数列”,使 ;若存在,求
;若存在,求