题目内容
已知函数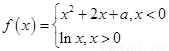 ,其中
,其中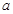 是实数,设
是实数,设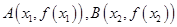 为该函数的图象上的两点,且
为该函数的图象上的两点,且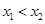 .
.
⑴指出函数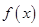 的单调区间;
的单调区间;
⑵若函数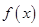 的图象在点
的图象在点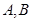 处的切线互相垂直,且
处的切线互相垂直,且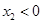 ,求
,求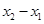 的最小值;
的最小值;
⑶若函数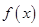 的图象在点
的图象在点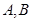 处的切线重合,求
处的切线重合,求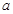 的取值范围.
的取值范围.
【答案】
(1)单调减区间为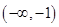 ,单调增区间为
,单调增区间为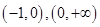 ;(2)1;(3)
;(2)1;(3)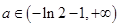 .
.
【解析】
试题分析:(1)根据基本初等函数的性质知,分段函数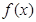 在
在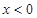 时是二次函数的一部分,有两个单调区间:增区间
时是二次函数的一部分,有两个单调区间:增区间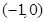 ,减区间
,减区间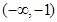 ,
,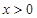 时是对数函数,只有一个单调增区间
时是对数函数,只有一个单调增区间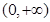 ;(2)对函数图象来讲,它在某点处的切线斜率等于该函数在此点处的导数,故有
;(2)对函数图象来讲,它在某点处的切线斜率等于该函数在此点处的导数,故有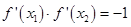 ,由于
,由于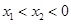 ,
,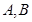 两点在
两点在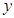 轴的左边,
轴的左边,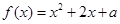 ,因此有
,因此有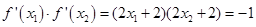 ,显然有
,显然有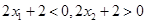 ,
, 可以表示为关于
可以表示为关于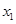 的函数,从而求出最小值(
的函数,从而求出最小值(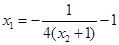 ,
,
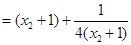 应用基本不等式即可得解)也可以直接凑配出基本不等式的形式,
应用基本不等式即可得解)也可以直接凑配出基本不等式的形式, =
=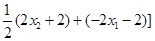 利用基本不等式);(3)这里我们首先分析
利用基本不等式);(3)这里我们首先分析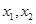 所处范围,结合图象易知
所处范围,结合图象易知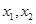 不可能在同一单调区间,只能是
不可能在同一单调区间,只能是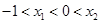 ,那么我们可得出
,那么我们可得出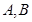 两点处的切线方程分别为
两点处的切线方程分别为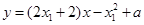 ,
,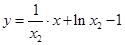 ,两条切线相同,则有
,两条切线相同,则有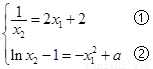 ,于是可把
,于是可把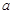 表示为
表示为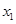 (或者
(或者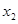 )的函数,把求
)的函数,把求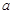 匠范围转化为求函数的值域.
匠范围转化为求函数的值域.
试题解析:(1)单调减区间为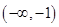 ,单调增区间为
,单调增区间为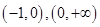 4分
4分
(2)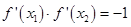 ,
,
当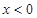 时,因为
时,因为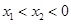 ,所以
,所以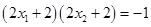 . 8分
. 8分
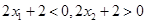
∴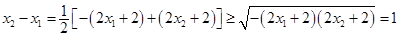
当且仅当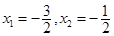 时等号成立,
时等号成立,
∴ 的最小值为1. 10分
的最小值为1. 10分
(3)当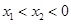 或
或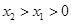 时,
时,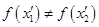 ,故
,故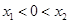
当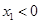 时,函数
时,函数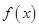 的图象在点
的图象在点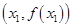 的切线方程为
的切线方程为
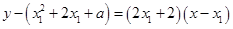
即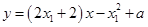
当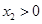 时,函数
时,函数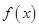 在
在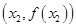 切线方程为
切线方程为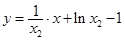
两切线重合的充要条件是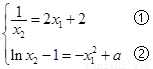 13分
13分
由①及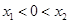 知
知
由①②得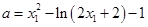
又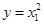 ,与
,与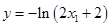 在
在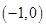 都为减函数.
都为减函数.
∴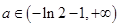 16分
16分
考点:(1)单调区间;(2)函数图象的切线及基本不等式;(3)切线与函数的值域.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
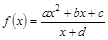 (其中
(其中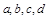 是实数常数,
是实数常数,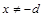 )
)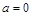 ,函数
,函数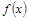 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求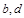 的值;
的值;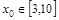 ,总有
,总有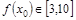 ,求
,求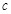 的取值范围;
的取值范围;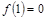 ,
,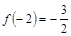 ,且对任意
,且对任意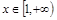 时,不等式
时,不等式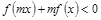 恒成立,求负实数
恒成立,求负实数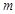 的取值范围.
的取值范围.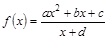 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.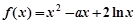 (其中
(其中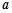 是实数).
是实数).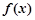 的单调区间;
的单调区间;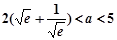 ,且
,且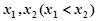 ,求
,求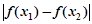 的取值范围.
的取值范围. 是自然对数的底数)
是自然对数的底数)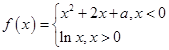 ,其中
,其中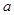 是实数,设
是实数,设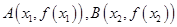 为该函数的图象上的两点,且
为该函数的图象上的两点,且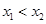 .
.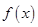 的单调区间;
的单调区间;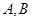 处的切线互相垂直,且
处的切线互相垂直,且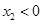 ,求
,求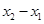 的最小值;
的最小值;