题目内容
过抛物线 的焦点的直线
的焦点的直线 与抛物线交于
与抛物线交于 、
、 两点,且
两点,且 (
( 为坐标原点)的面积为
为坐标原点)的面积为 ,则
,则 = .
= .

解析试题分析:先根据抛物线的方程求得焦点的坐标,代入直线方程求得 和
和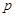 的关系式,进而把直线与抛物线方程联立消去
的关系式,进而把直线与抛物线方程联立消去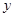 ,求得方程的解,进而根据直线方程可分别求得
,求得方程的解,进而根据直线方程可分别求得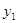 和
和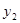 ,
, 的面积可分为
的面积可分为 与
与 的面积之和,而
的面积之和,而 与
与 若以
若以 为公共底,则其高即为
为公共底,则其高即为 、
、 两点的
两点的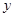 轴坐标的绝对值,进而可表示三角形的面积进而求得
轴坐标的绝对值,进而可表示三角形的面积进而求得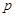 ,则
,则 的值可得,代入
的值可得,代入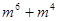 中,即可求得答案.
中,即可求得答案.
考点:椭圆的简单性质.

练习册系列答案
相关题目

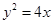 的准线方程为________.
的准线方程为________.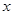 =-2y2的准线方程是 .
=-2y2的准线方程是 .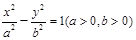 与圆x2+y2=a2+b2在第一象限的交点,其中F1,F2分别是双曲线的左、右焦点,且
与圆x2+y2=a2+b2在第一象限的交点,其中F1,F2分别是双曲线的左、右焦点,且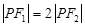 ,则双曲线的离心率为______.[来
,则双曲线的离心率为______.[来 的焦点作直线
的焦点作直线 交抛物线于A、B两点,若线段AB中点的横坐标为3,则|AB|等于( )
交抛物线于A、B两点,若线段AB中点的横坐标为3,则|AB|等于( ) =1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
=1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则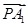 ·
· 的最小值为________.
的最小值为________. -
- =1上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则|PQ|-|PR|的最大值是________.
=1上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则|PQ|-|PR|的最大值是________.