题目内容
点P到点A(0,1),B(2,a)及直线y=-1的距离都相等,如果这样的点恰好只有一个,那么a的值是( )A.-1或1
B.1或0
C.0
D.1
【答案】分析:利用抛物线的定义求出P的方程,通过点P到点A(0,1),B(2,a)及直线y=-1的距离都相等,只需AB的中垂线与抛物线只有一个交点,即可求出a的值.
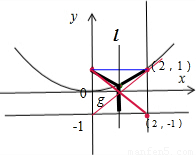
解答:解:点P到点A(0,1)及直线y=-1的距离都相等,所以P的轨迹是抛物线,x2=4y,因为点P到点A(0,1),B(2,a)及直线y=-1的距离都相等,AB的中垂线与抛物线只有一个交点,如图中的直线l与抛物线只有一个交点,a=1;
图中g与抛物线相切,g的方程:y=x-1,与x2=4y联立,可得x2-4x+4=0,△=0,满足题意,所以a=-1;
综上a=-1,a=1;
故选A.
点评:本题是中档题,考查抛物线的定义,数形结合的思想,抛物线的性质,考查计算能力,转化思想.
解答:解:点P到点A(0,1)及直线y=-1的距离都相等,所以P的轨迹是抛物线,x2=4y,因为点P到点A(0,1),B(2,a)及直线y=-1的距离都相等,AB的中垂线与抛物线只有一个交点,如图中的直线l与抛物线只有一个交点,a=1;
图中g与抛物线相切,g的方程:y=x-1,与x2=4y联立,可得x2-4x+4=0,△=0,满足题意,所以a=-1;
综上a=-1,a=1;

故选A.
点评:本题是中档题,考查抛物线的定义,数形结合的思想,抛物线的性质,考查计算能力,转化思想.

练习册系列答案
相关题目
点P是抛物线y2=4x上一动点,则点P到点A(0,-1)的距离与到直线x=-1的距离和的最小值是( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|