题目内容
已知点p是抛物线x=
y2上一个动点,则点p到点A(0,-1)的距离与点p到直线x=-1的距离和的最小值是 .
| 1 | 4 |
分析:利用抛物线的定义可知:当且仅当三点P,A,F共线时,|PF|+|PA|取得最小值|,利用两点间的距离公式即可得出.
解答:解:如图所示,过点P作PM⊥直线x=-1,垂垂足为M.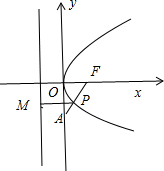
设抛物线的焦点为F,则F(1,0),|PF|=|PM|.
∴|PM|+|PA|=|PF|+|PA|,
当且仅当三点P,A,F共线时,|PF|+|PA|取得最小值|AF|=
=
.
故答案为:
.

设抛物线的焦点为F,则F(1,0),|PF|=|PM|.
∴|PM|+|PA|=|PF|+|PA|,
当且仅当三点P,A,F共线时,|PF|+|PA|取得最小值|AF|=
| 1+1 |
| 2 |
故答案为:
| 2 |
点评:本题考查了抛物线的定义、两点间的距离公式、三点共线与最小值问题,属于中档题.

练习册系列答案
相关题目
已知点P是抛物线y2=4x上一点,设点P到此抛物线准线的距离为d1,到直线x+2y+10=0的距离为d2,则d1+d2的最小值是( )
| A、5 | ||||
| B、4 | ||||
C、
| ||||
D、
|
已知点P是抛物线C:y=
x2上的动点,直线l:y=x-2,则点P到直线l的最短距离为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|