题目内容
7．求值：$\frac{tan（-150°）cos（-210°）cos660°}{tan（-240°）sin（-330°）}$．分析 运用诱导公式化简后根据特殊角的三角函数值即可求值．
解答 解：$\frac{tan（-150°）cos（-210°）cos660°}{tan（-240°）sin（-330°）}$=$\frac{tan30°（-cos30°）cos60°}{（-tan60°）sin30°}$=$\frac{\sqrt{3}}{6}$．
点评 本题主要考查了诱导公式，特殊角的三角函数值在化简求值中的应用，属于基本知识的考查．
练习册系列答案
百年学典课时学练测系列答案
相关题目
9．
已知奇函数$y=\left\{\begin{array}{l}f（x），\;\;x＞0\\ g（x），\;\;x＜0.\end{array}\right.$如果f（x）=ax（a＞0且a≠1）对应的图象如图所示，那么g（x）=（ ）
已知奇函数$y=\left\{\begin{array}{l}f（x），\;\;x＞0\\ g（x），\;\;x＜0.\end{array}\right.$如果f（x）=ax（a＞0且a≠1）对应的图象如图所示，那么g（x）=（ ）| A． | ${（\frac{1}{2}）^{-x}}$ | B． | $-{（\frac{1}{2}）^x}$ | C． | 2-x | D． | -2x |
如图，在四棱锥P-ABCD中，已知底面ABCD是平行四边形，且PA⊥底面ABCD，BD⊥PC，E是PA的中点．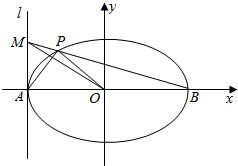
在平面直角坐标系xOy中，已知椭圆C：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0），的离心率为$\frac{{\sqrt{2}}}{2}$，且经过点（1，$\frac{{\sqrt{6}}}{2}$），过椭圆的左顶点A作直线l⊥x轴，点M为直线l上的动点（点M与点A在不重合），点B为椭圆右顶点，直线BM交椭圆C于点P．
16．“m＞2”是“直线y=kx+2k与圆x2+y2+mx=0至少有一个交点”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
