题目内容
15. 如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.
如图,在四棱锥P-ABCD中,已知底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.(1)求证:平面PAC⊥平面EBD;
(2)若PA=AB=AC=2,求三棱锥P-EBD的高.
分析 (1)首先根据线面的垂直转化成线线垂直,进一步利用线面垂直的判定得到线面垂直,进一步转化成面面垂直.
(2)利用(1)的结论得到平行四边形ABCD为菱形,进一步求出${S}_{△ABD}=\sqrt{3}$和${S}_{△EBD}=\sqrt{6}$,最后利用锥体的体积公式求出锥体的高.
解答 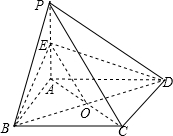 证明:(1)在四棱锥P-ABCD中,已知底面ABCD是平行四边形,且PA⊥底面ABCD,
证明:(1)在四棱锥P-ABCD中,已知底面ABCD是平行四边形,且PA⊥底面ABCD,
BD?平面ABCD,
则:PA⊥BD,
又BD⊥PC,
所以:BD⊥平面PAC.
由于BD?平面EBD,
所以:平面PAC⊥平面EBD.
(2)由(1)得到:BD⊥平面PAC,
所以:BD⊥AC.
所以:平行四边形ABCD为菱形.
由于PA=AB=AC=2,
所以:∠BAD=120°,
S△ABD=$\frac{1}{2}AC•\frac{1}{2}BD$=$\sqrt{3}$
E是PA的中点.连接OE,
得到:BD⊥OE.
所以:PC=$\sqrt{{PA}^{2}+{AC}^{2}}=2\sqrt{2}$,
所以:$OE=\frac{1}{2}PC=\sqrt{2}$,
S△EBD=$\frac{1}{2}$BD•OE=$\sqrt{6}$.
设三棱锥P-EBD的高为h,则:VP-EBD=VE-ABD,
$\frac{1}{3}{S}_{△EBD}•h=\frac{1}{3}{S}_{△ABD}•AE$,
解得:h=$\frac{\sqrt{2}}{2}$.
点评 本题考查的知识要点:线面垂直的判定定理和面面垂直的判定定理,锥体的体积公式的应用.及相关的运算问题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
17.将函数$y=cos(\frac{1}{2}x-\frac{π}{6})$图象向左平移$\frac{π}{3}$个长度单位,再把所得图象上各点的横坐标缩短到原来的一半(纵坐标不变),所得图象的函数解析式是( )
| A. | $y=cos(x+\frac{π}{6})$ | B. | $y=cos\frac{1}{4}x$ | C. | y=cosx | D. | $y=cos(\frac{1}{4}x-\frac{π}{3})$ |
5.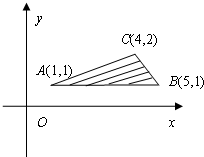 在如图所示的坐标平面的可行域内(阴影部分且包括边界),若目标函数z=x+ay取得最小值的最优解有无数个,则$\frac{y}{x-a}$的最大值是( )
在如图所示的坐标平面的可行域内(阴影部分且包括边界),若目标函数z=x+ay取得最小值的最优解有无数个,则$\frac{y}{x-a}$的最大值是( )
 在如图所示的坐标平面的可行域内(阴影部分且包括边界),若目标函数z=x+ay取得最小值的最优解有无数个,则$\frac{y}{x-a}$的最大值是( )
在如图所示的坐标平面的可行域内(阴影部分且包括边界),若目标函数z=x+ay取得最小值的最优解有无数个,则$\frac{y}{x-a}$的最大值是( )| A. | $\frac{2}{7}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |