题目内容
已知函数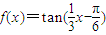
(1)求f(x)的最小正周期;
(2)求
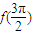 的值;
的值;(3)设
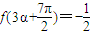 ,求
,求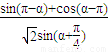 的值.
的值.
【答案】分析:(1)找出ω的值,代入周期公式即可求出函数的最小正周期;
(2)将x=3α+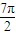 代入函数解析式,根据已知等式利用诱导公式化简求出tanα的值,所求式子利用诱导公式变形后,分子分母除以cosα,利用同角三角函数间的基本关系弦化切变形后,将tanα的值代入计算即可求出值.
代入函数解析式,根据已知等式利用诱导公式化简求出tanα的值,所求式子利用诱导公式变形后,分子分母除以cosα,利用同角三角函数间的基本关系弦化切变形后,将tanα的值代入计算即可求出值.
解答:解:(1)f(x)的最小正周期为T=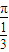 =3π;
=3π;
(2)将x=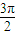 代入得:f(
代入得:f(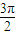 )=tan(
)=tan(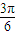 -
-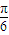 )=tan
)=tan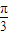 =
=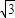 ;
;
(3)由f(3α+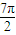 )=-
)=- ,得tan[
,得tan[ (3α+
(3α+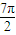 )-
)-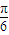 ]=-
]=- ,即tan(π+α)=-
,即tan(π+α)=- ,
,
∴tanα=- ,
,
∵cosα≠0,
则原式=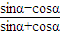 =
=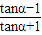 =
=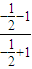 =-3.
=-3.
点评:此题考查了三角函数的周期性及其求法,同角三角函数间的基本关系的运用,以及诱导公式的作用,熟练掌握公式是解本题的关键.
(2)将x=3α+
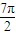 代入函数解析式,根据已知等式利用诱导公式化简求出tanα的值,所求式子利用诱导公式变形后,分子分母除以cosα,利用同角三角函数间的基本关系弦化切变形后,将tanα的值代入计算即可求出值.
代入函数解析式,根据已知等式利用诱导公式化简求出tanα的值,所求式子利用诱导公式变形后,分子分母除以cosα,利用同角三角函数间的基本关系弦化切变形后,将tanα的值代入计算即可求出值.解答:解:(1)f(x)的最小正周期为T=
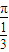 =3π;
=3π;(2)将x=
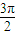 代入得:f(
代入得:f(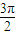 )=tan(
)=tan(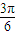 -
-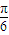 )=tan
)=tan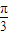 =
=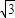 ;
;(3)由f(3α+
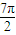 )=-
)=- ,得tan[
,得tan[ (3α+
(3α+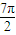 )-
)-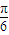 ]=-
]=- ,即tan(π+α)=-
,即tan(π+α)=- ,
,∴tanα=-
 ,
,∵cosα≠0,
则原式=
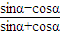 =
=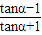 =
=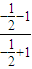 =-3.
=-3.点评:此题考查了三角函数的周期性及其求法,同角三角函数间的基本关系的运用,以及诱导公式的作用,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目


 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.

