题目内容
已知函数
(1)求f(1),f(-3),f(a+1)的值;
(2)求函数f(x)的零点.
【答案】分析:(1)将x=1,-3,a+1代入函数解析式即可求出答案;(2)令f(x)=0,求出方程的两个根,最后根据方程的根就是函数的零点即可求得.
解答:解:(1)因为1>0,所以f(1)=12+4×1-2=3;
因为-3<0,所以f(-3)=(-3)2-4×(-3)-2=19;
当a+1≥0,即a≥-1时,f(a+1)=(a+1)2+4(a+1)-2=a2+6a+3;
当a+1<0,即a<-1时,f(a+1)=(a+1)2-4(a+1)-2=a2-2a-5.
(2)由题意,得 ,解得
,解得 ;
;
或 ,解得
,解得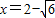 .
.
所以函数f(x)的零点为 与
与 .
.
点评:本题主要考查了函数的零点问题,和求函数值,以及函数零点与方程根的关系,考查运算能力,属于基础题.
解答:解:(1)因为1>0,所以f(1)=12+4×1-2=3;
因为-3<0,所以f(-3)=(-3)2-4×(-3)-2=19;
当a+1≥0,即a≥-1时,f(a+1)=(a+1)2+4(a+1)-2=a2+6a+3;
当a+1<0,即a<-1时,f(a+1)=(a+1)2-4(a+1)-2=a2-2a-5.
(2)由题意,得
 ,解得
,解得 ;
;或
 ,解得
,解得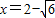 .
.所以函数f(x)的零点为
 与
与 .
.点评:本题主要考查了函数的零点问题,和求函数值,以及函数零点与方程根的关系,考查运算能力,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目


 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围.
