题目内容
(本小题满分12分)已知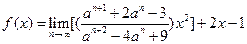
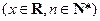 ,设
,设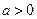 ,
,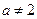 .(Ⅰ)求出函数
.(Ⅰ)求出函数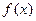 的解析式;(Ⅱ)是否存在
的解析式;(Ⅱ)是否存在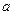 使得函数
使得函数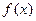 能以
能以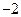 为其最小值?若能,求出对应的
为其最小值?若能,求出对应的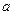 的取值或取值范围;若不能,试说明理由.
的取值或取值范围;若不能,试说明理由.
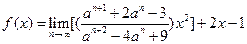
 ,设
,设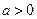 ,
,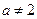 .(Ⅰ)求出函数
.(Ⅰ)求出函数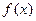 的解析式;(Ⅱ)是否存在
的解析式;(Ⅱ)是否存在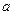 使得函数
使得函数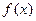 能以
能以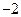 为其最小值?若能,求出对应的
为其最小值?若能,求出对应的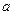 的取值或取值范围;若不能,试说明理由.
的取值或取值范围;若不能,试说明理由.(Ⅰ)
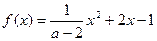 (Ⅱ)
(Ⅱ)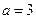

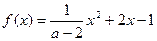 (Ⅱ)
(Ⅱ)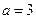
(Ⅰ)∵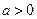 ,∴当
,∴当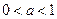 时
时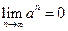 ,
,
∴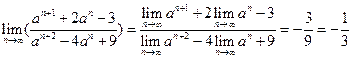 ,
,
此时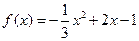 ,函数图象开口向下,没有最小值; …………3分
,函数图象开口向下,没有最小值; …………3分
当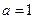 时,
时,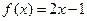 ,函数单调递增,此时也没有最小值; …………5分
,函数单调递增,此时也没有最小值; …………5分
当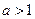 且
且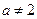 时
时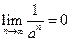 ,∴
,∴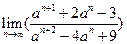
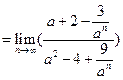
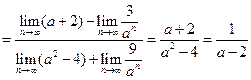 ,
,
此时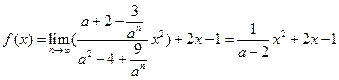 ;…8分
;…8分
(Ⅱ)若 即
即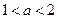 时,函数
时,函数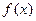 开口向下,没有最小值,
开口向下,没有最小值,
而当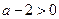 即
即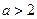 时,函数
时,函数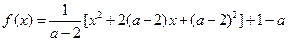 ,
,
当且仅当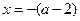 时有最小值
时有最小值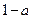 , 令
, 令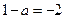 ,则
,则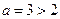 ,
,
∴存在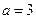 恰使函数
恰使函数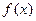 以
以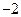 为其最小值.……12分
为其最小值.……12分
本题考查极限的概念、数列极限的求法、重要极限的应用、二次函数的最值及分类讨论的思想方法,属易错题、难题
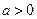 ,∴当
,∴当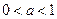 时
时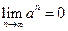 ,
,∴
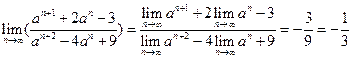 ,
,此时
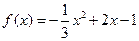 ,函数图象开口向下,没有最小值; …………3分
,函数图象开口向下,没有最小值; …………3分当
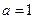 时,
时,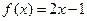 ,函数单调递增,此时也没有最小值; …………5分
,函数单调递增,此时也没有最小值; …………5分当
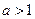 且
且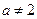 时
时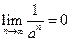 ,∴
,∴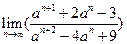
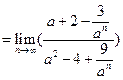
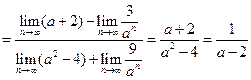 ,
,此时
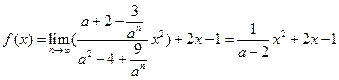 ;…8分
;…8分(Ⅱ)若
 即
即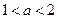 时,函数
时,函数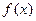 开口向下,没有最小值,
开口向下,没有最小值,而当
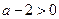 即
即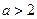 时,函数
时,函数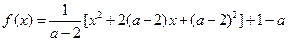 ,
,当且仅当
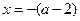 时有最小值
时有最小值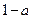 , 令
, 令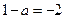 ,则
,则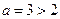 ,
,∴存在
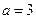 恰使函数
恰使函数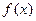 以
以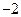 为其最小值.……12分
为其最小值.……12分本题考查极限的概念、数列极限的求法、重要极限的应用、二次函数的最值及分类讨论的思想方法,属易错题、难题

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
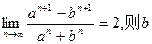 的取值范围是
的取值范围是 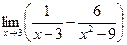


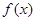 的图象是连续不断的,有如下
的图象是连续不断的,有如下 、
、 上的零点至少有( )个
上的零点至少有( )个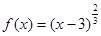 ,点
,点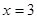 是
是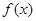 的
的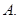 连续不可导点
连续不可导点 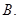 可导不连续点
可导不连续点 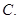 可导且连续点
可导且连续点 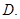 非极值点
非极值点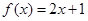 ,则
,则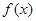 在区间
在区间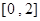 上的平均变化率为 .
上的平均变化率为 .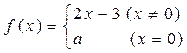 在
在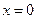 处连续,则
处连续,则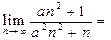 ( )
( )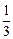
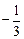
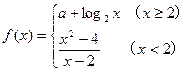 在x=2处连续,则常数
在x=2处连续,则常数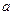 的值是 ( )
的值是 ( )