��Ŀ����
����Ŀ��M����ԲT��![]() 1��a��b��0��������һ�㣬F����ԲT���ҽ��㣬AΪ�㣬BΪ�϶��㣬OΪ����ԭ�㣬����ͼ��ʾ����֪|MF|�����ֵΪ3
1��a��b��0��������һ�㣬F����ԲT���ҽ��㣬AΪ�㣬BΪ�϶��㣬OΪ����ԭ�㣬����ͼ��ʾ����֪|MF|�����ֵΪ3![]() ������MAF������ֵΪ3
������MAF������ֵΪ3![]() ��
��
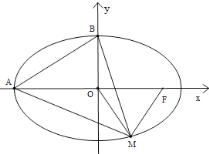
��1������ԲT�ı�����
��2������ABM����������ֵS0������N��x��y������x��Z��y��Z���Ƶ�NΪ��㣮����ԲT�ڲ��Ƿ���ڸ��G��ʹ����ABG�����S�ʣ�6��S0���������ڣ����G�����꣬�������ڣ���˵�����ɣ�
���𰸡�(1)![]() (2)���ڣ�����Ϊ��2����1��
(2)���ڣ�����Ϊ��2����1��
��������
��1������Բ���ʿ�֪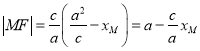 ������֪������
������֪������![]() ����
����![]() �����ֵΪ2����b=2�����a��b��c�Ĺ�ϵ�������ԲT�ķ��̣�
�����ֵΪ2����b=2�����a��b��c�Ĺ�ϵ�������ԲT�ķ��̣�
��2������ֱ֪��AB�ķ���Ϊ![]() ����ֱ��
����ֱ��![]() ����ԲT������x���·��ĵ�M0������ABM0�����Ϊ��ABM����������ֵS0��ֱ������Բ�������ֱ��AB��ֱ��l����Ϊ
����ԲT������x���·��ĵ�M0������ABM0�����Ϊ��ABM����������ֵS0��ֱ������Բ�������ֱ��AB��ֱ��l����Ϊ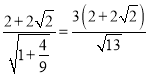 ���ɴ��������2����1��Ϊ������G��
���ɴ��������2����1��Ϊ������G��
��1������Բ���ʿ�֪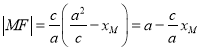 ��
��
����c��0��c2��a2��b2��
��ΪxM��[��a��a]����|MF|��[a��c��a+c]����![]()
����MAF������ֵΪ3![]() ����
���� ![]() ����
����![]() �����ֵΪ2����b=2����b2��a2��c2��
�����ֵΪ2����b=2����b2��a2��c2��![]()
��֮��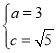
��ԲT�ķ���Ϊ![]()
��2������ֱ֪��AB�ķ���Ϊ![]() ��
��
��ֱ��![]() ����ԲT������x���·��ĵ�M0��
����ԲT������x���·��ĵ�M0��
���ABM0�����Ϊ��ABM����������ֵS0.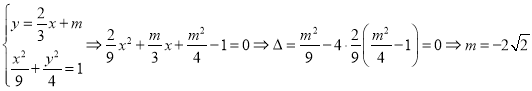
��ʱ��ֱ��AB��ֱ��l����Ϊ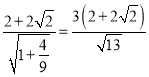 ��
��
��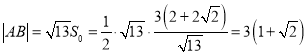
��![]() ����
����![]() ����
����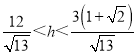
��ֱ��![]() ��ֱ��AB�ľ���Ϊ
��ֱ��AB�ľ���Ϊ![]() ��
��
����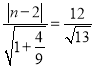 �����n����2��6��
�����n����2��6��
ע�l1��ֱ��ABƽ����l1������ԲTӦ�й����㣬
��ֻ�迼��n����2�����Σ�
ֱ��![]() ������ԲT���¶���B0��0����2�����Ҷ���A0��
������ԲT���¶���B0��0����2�����Ҷ���A0��
���߶�A0B0������һ��G0��A��B��ɵ������ε����Ϊ6
����������������������ĸ��G����G����ֱ��A0B0��l֮�䣮
������Բ�ڲ�λ�������ĸ��Ϊ��1����1������2����1��
��Ϊ![]() ���ʣ�1����1����ֱ��A0B0�Ϸ�����������
���ʣ�1����1����ֱ��A0B0�Ϸ�����������
��![]() ����㣨2����1����ֱ��A0B0�·���
����㣨2����1����ֱ��A0B0�·���
��![]() ��������Բ�ڲ���
��������Բ�ڲ���
���ԣ�2����1��Ϊ������G��