题目内容
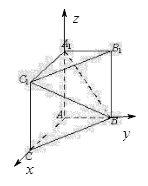
如图,在三棱柱ABC-A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5.
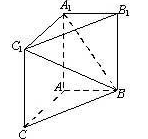
(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求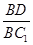 的值.
的值.

(Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求二面角A1-BC1-B1的余弦值;
(Ⅲ)证明:在线段BC1存在点D,使得AD⊥A1B,并求
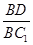 的值.
的值.(Ⅰ)见解析(Ⅱ)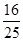 (Ⅲ)
(Ⅲ)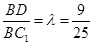
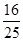 (Ⅲ)
(Ⅲ)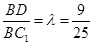
把平面与平面垂直转化为直线和平面垂直.要证直线和平面垂直,依据相关判定定理转化为证明直线和直线垂直.求二面角,往往利用“作——证——求”的思路完成,作二面角是常常利用直线和平面垂直.第(Ⅲ)题,求解有难度,可以空间向量完成.
(Ⅰ)因为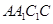 为正方形,所以
为正方形,所以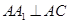 .
.
因为平面ABC⊥平面AA1C1C,,且平面ABC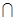 平面AA1C1C
平面AA1C1C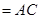 ,
,
所以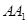 ⊥平面ABC.
⊥平面ABC.
(Ⅱ)由(Ⅰ)知,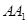 ⊥AC,
⊥AC, 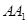 ⊥AB.
⊥AB.
由题意知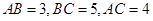 ,所以
,所以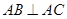 .
.
如图,以A为原点建立空间直角坐标系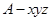 ,则
,则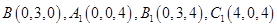 .
.
设平面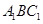 的法向量为
的法向量为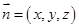 ,则
,则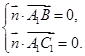 即
即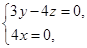
令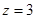 ,则
,则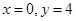 ,所以
,所以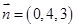 .
.
同理可得,平面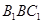 的法向量为
的法向量为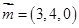 .
.
所以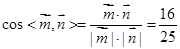 .
.
由题知二面角A1-BC1-B1为锐角,所以二面角A1-BC1-B1的余弦值为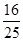 .
.
(Ⅲ)设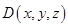 是直线
是直线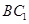 上的一点,且
上的一点,且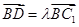 .
.
所以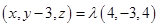 ,解得
,解得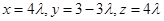 ,所以
,所以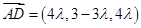 .
.
由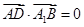 ,即
,即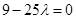 ,解得
,解得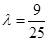 .
.
因为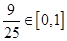 ,所以在线段
,所以在线段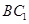 上存在点D,使得
上存在点D,使得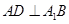 ,此时
,此时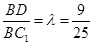 .
.
【考点定位】本题考查了平面与平面垂直的性质定理,直线和平面垂直的判定定理,考查了法向量、空间向量在立体几何中的应用和二面角的求法,考查了空间想象能力和推理论证能力.
(Ⅰ)因为
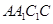 为正方形,所以
为正方形,所以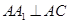 .
.因为平面ABC⊥平面AA1C1C,,且平面ABC
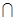 平面AA1C1C
平面AA1C1C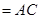 ,
,所以
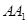 ⊥平面ABC.
⊥平面ABC.(Ⅱ)由(Ⅰ)知,
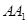 ⊥AC,
⊥AC, 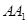 ⊥AB.
⊥AB.由题意知
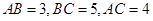 ,所以
,所以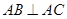 .
.如图,以A为原点建立空间直角坐标系
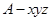 ,则
,则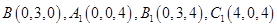 .
.设平面
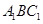 的法向量为
的法向量为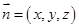 ,则
,则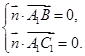 即
即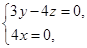
令
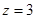 ,则
,则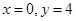 ,所以
,所以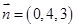 .
.同理可得,平面
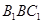 的法向量为
的法向量为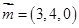 .
.所以
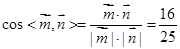 .
.由题知二面角A1-BC1-B1为锐角,所以二面角A1-BC1-B1的余弦值为
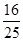 .
.
(Ⅲ)设
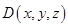 是直线
是直线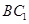 上的一点,且
上的一点,且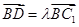 .
.所以
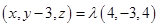 ,解得
,解得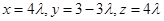 ,所以
,所以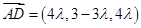 .
.由
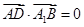 ,即
,即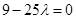 ,解得
,解得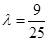 .
.因为
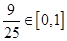 ,所以在线段
,所以在线段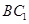 上存在点D,使得
上存在点D,使得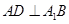 ,此时
,此时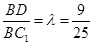 .
.【考点定位】本题考查了平面与平面垂直的性质定理,直线和平面垂直的判定定理,考查了法向量、空间向量在立体几何中的应用和二面角的求法,考查了空间想象能力和推理论证能力.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 的边长为4,
的边长为4, ,
, .将菱形
.将菱形 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点, .
.
 平面
平面 ;
;
 平面
平面 ;
; 的余弦值.
的余弦值.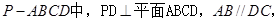
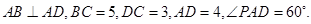
 的方向相同时,画出四棱锥
的方向相同时,画出四棱锥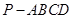 的正视图(要求标出尺寸,并写出演算过程);
的正视图(要求标出尺寸,并写出演算过程);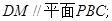
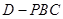 的体积.
的体积.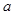 、
、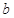 是两条不同的直线,
是两条不同的直线,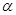 、
、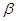 是两个不同的平面,给出下列结论:
是两个不同的平面,给出下列结论: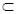
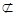
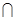
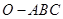 的侧棱
的侧棱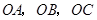 两两垂直,且
两两垂直,且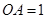 ,
,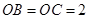 ,
,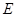 是
是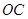 的中点.
的中点.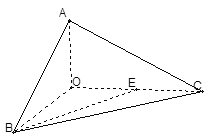
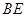 与
与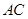 所成的角的余弦值
所成的角的余弦值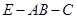 的余弦值
的余弦值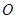 点到面
点到面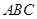 的距离
的距离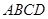 中,
中,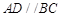 ,
,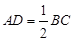 ,
,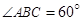 ,
,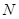 是
是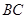 的中点.将梯形
的中点.将梯形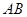 旋转
旋转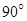 ,得到梯形
,得到梯形 (如图).
(如图).
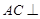 平面
平面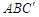 ;
; 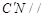 平面
平面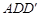 ;
;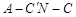 的余弦值.
的余弦值.
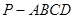 中,底面
中,底面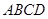 是正方形,
是正方形, 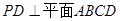 ,
,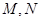 分别为
分别为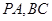 的中点,且
的中点,且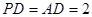 .
.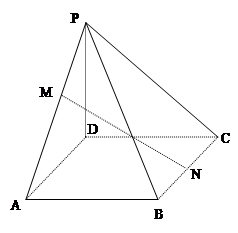
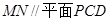 ;
;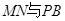 所成的角的余弦值
所成的角的余弦值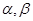 和直线
和直线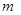 ,给出条件:①
,给出条件:①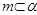 ;②
;②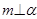 ;③
;③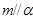 ;④
;④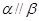 ;⑤
;⑤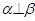 .为使
.为使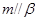 ,应选择下面四个选项中的条件( )
,应选择下面四个选项中的条件( )