题目内容
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.
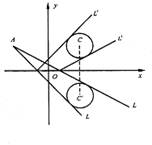
解法一:如图,已知圆的标准方程是:(x-2)2+(y-2)2=1,它关于x轴的对称圆的方程是(x-2)2+(y+2)2=1.设光线L所在的直线的方程是y-3=k(x+3)(其中斜率k待定),由题设知对称圆的圆心C′(2,-2)到这条直线的距离等于1,即d=![]() =1.整理得:12k2+25k+12=0,解得k= -
=1.整理得:12k2+25k+12=0,解得k= -![]() 或k= -
或k= -![]() .故所求直线方程是y-3= -
.故所求直线方程是y-3= -![]() (x+3),或y-3= -
(x+3),或y-3= -![]() (x+3),即3x+4y+3=0或4x+3y+3=0.
(x+3),即3x+4y+3=0或4x+3y+3=0.
解法二:已知圆的标准方程是:(x-2)2+(y-2)2=1,设光线L所在的直线的方程是:y-3=k(x+3)(其中斜率k待定),由题意知k≠0,则L的反射点的坐标是(-![]() ,0),因为光线的入射角等于反射角,所以反射光线
,0),因为光线的入射角等于反射角,所以反射光线![]() 所在直线的方程为y= -k(x+
所在直线的方程为y= -k(x+![]() ),即y+kx+3(1+k)=0.这条直线与已知圆相切,故圆心到直线的距离为1,即d=
),即y+kx+3(1+k)=0.这条直线与已知圆相切,故圆心到直线的距离为1,即d=![]() =1.以下同解法一.
=1.以下同解法一.
解析:
同答案

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
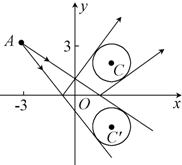 自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.

