题目内容
自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线l所在直线的方程.
【探究】 (1)如图所示,设l和x轴交于B(b,0),则kAB=![]() ,根据光的反射定律,反射线的斜率k反=
,根据光的反射定律,反射线的斜率k反=![]() ,
,
∴反射线所在的直线方程为
y=![]() (x-b).
(x-b).
即 3x-(b+3)y-3b=0.
∵已知圆x2+y2-4x-4y+7=0的圆心为C(2,2),半径为1,
∴![]() .解得b1=
.解得b1=![]() ,b2=1.
,b2=1.
∴kAB=![]() 或kAB=
或kAB=![]() .
.
∴l的方程为4x+3y+3=0或3x+4y-3=0.
(2)已知圆C:x2+y2-4x-4y+7=0关于x轴对称的圆为C1:(x-2)2+(y+2)2=1,其圆心C1的坐标为(2,-2),半径为1,由光的反射定律知,入射光线所在直线方程与圆C1相切.
设l的方程为y-3=k(x+3),则![]() ,
,
即 12k2+25k+12=0.∴k1=![]() ,k2=
,k2=![]() .
.
则l的方程为4x+3y+3=0或3x+4y-3=0.
(3)设入射光线方程为y-3=k(x+3),反射光线所在直线方程为y=-kx+b,由于二者横截距相等,且后者与已知圆相切,
∴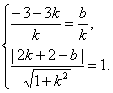
消去b得![]() =1(以下与解析(2)同).
=1(以下与解析(2)同).
【规律总结】 本题是方程思想的典型应用,考查的重点在于设置怎样的未知数,依怎样的性质列方程,解析(1)、(2)属常规方法,解析(3)设置两个未知数,体现了方程的方法在具体运用时的灵活性.

练习册系列答案
相关题目
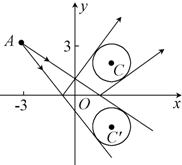 自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.
自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在直线的方程.
