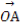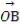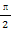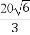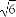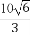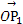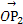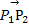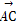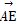Question

平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足=α+β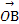,其中α,β∈R且α+β=1,则点C的轨迹方程为(　　)

(A)(x-1)2+(y-2)2=5(B)3x+2y-11=0

(C)2x-y=0(D)x+2y-5=0

 

Answer 1

D

【解析】【思路点拨】求轨迹方程的问题时可求哪个点的轨迹设哪个点的坐标,故设C(x,y),根据向量的运算法则及向量相等的关系,列出关于α,β,x,y的关系式,消去α,β即可得解.

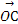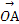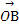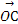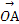解:设C(x,y),则=(x,y),=(3,1),=(-1,3).由=α+β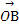,得(x,y)=(3α,α)+(-β,3β)=(3α-β,α+3β).

于是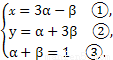

由③得β=1-α代入①②,消去β得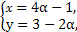

再消去α得x+2y=5,即x+2y-5=0.

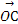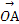【一题多解】由平面向量共线定理,得当=α+β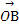,α+β=1时,A,B,C三点共线.

因此,点C的轨迹为直线AB,

由两点式求直线方程得=,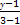

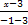即x+2y-5=0.