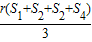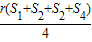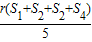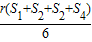题目内容
若△ABC的三边之长分别为a、b、c,内切圆半径为r,则△ABC的面积为 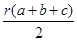 .根
.根 据类比思想可得:若四面体A-BCD的三个侧面与底面的面积分别为
据类比思想可得:若四面体A-BCD的三个侧面与底面的面积分别为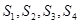 ,内切球的半径为r,则四面体的体积为( )
,内切球的半径为r,则四面体的体积为( )
A.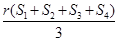 | B. | C.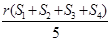 | D.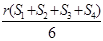 |
A
解析试题分析:根据三角形的边应与四面体中的各个面进行类比,而面积与体积进行类比,进行猜想. 解:根据几何体和平面图形的类比关系,三角形的边应与四面体中的各个面进行类比,而面积与体积进行类比:∴△ABC的面积为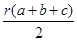 ,对应于四面体的体积为
,对应于四面体的体积为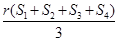 ,故选A
,故选A
考点:类比推理
点评:本题考察了立体几何和平面几何的类比推理,一般平面图形的边、面积分别于几何体中的面和体积进行类比,从而得到结论

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
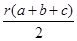 .根据类比思想可得:若四面体A-BCD的三个侧面与底面的面积分别为
.根据类比思想可得:若四面体A-BCD的三个侧面与底面的面积分别为 ,内切球的半径为r,则四面体的体积为( )
,内切球的半径为r,则四面体的体积为( ) B.
B.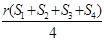 C.
C.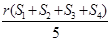 D.
D.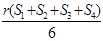
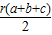 .根据类比思想可得:若四面体A-BCD的三个侧面与底面的面积分别为S1、S2、S3、S4,内切球的半径为r,则四面体的体积为( )
.根据类比思想可得:若四面体A-BCD的三个侧面与底面的面积分别为S1、S2、S3、S4,内切球的半径为r,则四面体的体积为( )