题目内容
已知各项都为正数的等比数列,{an}的公比q≠1,且a4,a6,a7成等差数列,则
的值等于:( )
| a4+a6 |
| a5+a7 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
分析:先用a4表示出a6、a7,然后根据a4,a6,a7成等差数列可得a4+a7=2a6,将a6、a7用a4的关系式代入,可求出q的值,根据
=
可得到答案.
| a4+a6 |
| a5+a7 |
| 1 |
| q |
解答:解:设a4=m,公比为q,所以a6=mq2,a7=mq3
a4+a7=2a6
m+mq3=2mq2
1+q3=2q2
(q-1)(q2-q-1)=0∵q≠1
∴q2-q-1=0∴q=
或
(舍)
∴
=
=
=
故选A.
a4+a7=2a6
m+mq3=2mq2
1+q3=2q2
(q-1)(q2-q-1)=0∵q≠1
∴q2-q-1=0∴q=
1+
| ||
| 2 |
1-
| ||
| 2 |
∴
| a4+a6 |
| a5+a7 |
| 1 |
| q |
| 2 | ||
1+
|
| ||
| 2 |
故选A.
点评:本题主要考查等比数列的基本性质.属基础题.

练习册系列答案
相关题目
 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈ ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是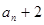 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈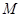 ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数 是an+2 和an的等比中项.
是an+2 和an的等比中项. +
+ +…+
+…+ <1;
<1; 恒成立,求这样的正整数m共有多少个?
恒成立,求这样的正整数m共有多少个?