题目内容
(本小题满分12分)
设数列 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是 和
和 的等比中项.
的等比中项.
(Ⅰ)证明数列 为等差数列,并求数列
为等差数列,并求数列 的通项公式;
的通项公式;
(Ⅱ)证明 ;
;
(Ⅲ)设集合 ,
, ,且
,且 ,若存在
,若存在 ∈
∈ ,使对满足
,使对满足 的一切正整数
的一切正整数 ,不等式
,不等式 恒成立,求这样的正整数
恒成立,求这样的正整数 共有多少个?
共有多少个?
解:(Ⅰ)由已知, ,且
,且 . ………………………1分
. ………………………1分
当 时,
时, ,解得
,解得 . ……………………………2分
. ……………………………2分
当 时,有
时,有 .
.
于是 ,
, 即
即 .
.
于是 ,即
,即 .
.
因为 ,所以
,所以 .
.
故数列 是首项为2,公差为2的等差数列,且
是首项为2,公差为2的等差数列,且 .……………………4分
.……………………4分
(Ⅱ)因为 ,则
,则 ,…………………………………5分
,…………………………………5分
所以
 …7分
…7分
(Ⅲ)由 ,得
,得 ,所以
,所以 . …… 9分
. …… 9分
由题设, ,
, ,…,
,…, ,
, ,
, ,
, …,
…,
 .
.
因为 ∈M,所以
∈M,所以 ,
, ,…,
,…, 均满足条件.…………………10分
均满足条件.…………………10分
且这些数组成首项为 ,公差为
,公差为 的等差数列.
的等差数列.
设这个等差数列共有 项,则
项,则 ,解得
,解得 .
.
故集合M中满足条件的正整数 共有450个.…………………………12分
共有450个.…………………………12分
解析

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
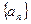 的首项为
的首项为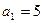 ,前
,前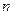 项和为
项和为 ,且
,且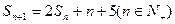
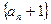 成等比数列;
成等比数列;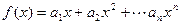 ,求函数
,求函数 在点
在点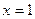 处的导数
处的导数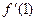 .
.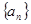 的首项为
的首项为 ,前
,前 项和为
项和为 ,且
,且
 成等比数列;
成等比数列; ,求函数
,求函数 在点
在点 处的导数
处的导数 .
. 的各项都为正数,其前
的各项都为正数,其前 项和为
项和为 ,已知对任意
,已知对任意 ,
, 是
是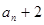 和
和 的等比中项.
的等比中项. 的通项公式;
的通项公式; ;
; ,
, ,且
,且 ,若存在
,若存在 ∈
∈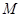 ,使对满足
,使对满足 的一切正整数
的一切正整数 恒成立,求这样的正整数
恒成立,求这样的正整数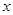 公里.经预算,修建一个轻轨中间站的费用为2000万元,修建
公里.经预算,修建一个轻轨中间站的费用为2000万元,修建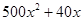 )万元.设余下工程的总费用为
)万元.设余下工程的总费用为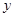 万元.
万元.