题目内容
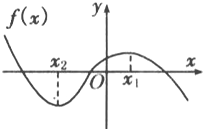
函数f(x)=ax3+bx2+cx+d的图象如图,且|x1|<|x2|,则有( )

| A、a>0,b>0,c<0,d>0 | B、a<0,b>0,c<0,d>0 | C、a>0,b<0,c>0,d<0 | D、a<0,b<0,c>0,d>0 |
分析:由图知二个零点x1,x2.从而得导函数f′(x)=3ax2+2bx+c的图象是开口向下、与x轴交于点(x1,0)、(x2,0)的抛物线,又由图得a<0,从而可以判断a,b,c的符号,再由图象与y轴的交点即可得到d的符号.
解答:解:由图象可知:
则导函数f′(x)=3ax2+2bx+c的图象是开口向下、与x轴交于点(x1,0)、(x2,0)的抛物线
故a<0,
又由x2<0,x1>0,且|x1|<|x2|知:x1+x2=-
<0,x1x2=
<0
∴b<0,c>0,
又由图象可知,f(0)=d>0,
则a<0,b<0,c>0,d>0,
故选:D.
| x | (-∞,x2) | x2 | (x2,x1) | x1 | (x1,+∞) |
| f(x) | ↘ | 极小值 | ↗ | 极大值 | ↘ |
| f′(x) | - | 0 | + | 0 | - |
故a<0,
又由x2<0,x1>0,且|x1|<|x2|知:x1+x2=-
| 2b |
| 3a |
| c |
| 3a |
∴b<0,c>0,
又由图象可知,f(0)=d>0,
则a<0,b<0,c>0,d>0,
故选:D.
点评:本题考查函数的零点,三次函数的图象,以及利用图象解决问题的能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目