题目内容
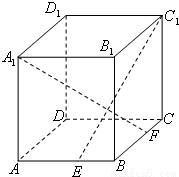
 如图,ABCD-A1B1C1D1是正四棱柱,则棱长为3,底面边长为2,E是棱BC的中点.
如图,ABCD-A1B1C1D1是正四棱柱,则棱长为3,底面边长为2,E是棱BC的中点.(Ⅰ)求证:BD1∥平面C1DE;
(Ⅱ)求二面角C1-DE-C的大小;
(Ⅲ)在侧棱BB1上是否存在点P,使得CP⊥平面C1DE?证明你的结论.
【答案】分析:(I)连接CD1,与C1D相交于O,连接EO,要证BD1∥平面C1DE,直线证明BD1平行平面C1DE内的直线EO即可;
(II)过点C作CH⊥DE于H,连接C1H,说明∠C1HC是二面角C1-DE-C的平面角,然后求二面角C1-DE-C的大小;
(III)用反证法证明在侧棱BB1上不存在点P,使得CP⊥平面C1DE,推出矛盾即可.
解答: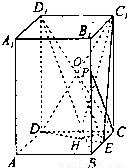 解:(I)证明:连接CD1,与C1D相交于O,连接EO.
解:(I)证明:连接CD1,与C1D相交于O,连接EO.
∵CDD1C1是矩形,
∴O是CD1的中点,
又E是BC的中点,
∴EO∥BD1.(2分)
又BD1?平面C1DE,EO?平面C1DE,
∴BD1∥平面C1DE.(4分)
(II)解:过点C作CH⊥DE于H,连接C1H.
在正四棱柱ABCD-A1B1C1D1中,CC1⊥平面ABCD,
∴C1H⊥DE,
∠C1HC是二面角C1-DE-C的平面角.(7分)
根据平面几何知识,易得H(0.8,1.6,0)
.∴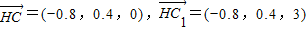 ,
,
∵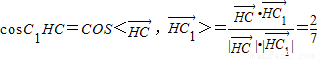 (9分)
(9分)
∴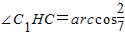 ,
,
∴二面角C1-DE-C的大小为ArCCOs .(10分)
.(10分)
(III)解:在侧棱BB1上不存在点P,使得CP⊥平面C1DE(11分)
证明如下:
假设CP⊥平面C1DE,则必有CP⊥DE.
设P(2,2,a),其中0≤a≤3,
则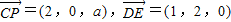 ,
,
∵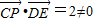 ,这显然与CP⊥DE矛盾.
,这显然与CP⊥DE矛盾.
∴假设CP⊥平面C1DE不成立,
即在侧棱BB1上不存在点P,使得CP⊥平面C1DE.(14分)
点评:本题考查直线与平面的存在,二面角的求法等知识,考查空间想象能力,逻辑思维能力,是中档题.
(II)过点C作CH⊥DE于H,连接C1H,说明∠C1HC是二面角C1-DE-C的平面角,然后求二面角C1-DE-C的大小;
(III)用反证法证明在侧棱BB1上不存在点P,使得CP⊥平面C1DE,推出矛盾即可.
解答:
 解:(I)证明:连接CD1,与C1D相交于O,连接EO.
解:(I)证明:连接CD1,与C1D相交于O,连接EO.∵CDD1C1是矩形,
∴O是CD1的中点,
又E是BC的中点,
∴EO∥BD1.(2分)
又BD1?平面C1DE,EO?平面C1DE,
∴BD1∥平面C1DE.(4分)
(II)解:过点C作CH⊥DE于H,连接C1H.
在正四棱柱ABCD-A1B1C1D1中,CC1⊥平面ABCD,
∴C1H⊥DE,
∠C1HC是二面角C1-DE-C的平面角.(7分)
根据平面几何知识,易得H(0.8,1.6,0)
.∴
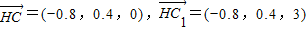 ,
,∵
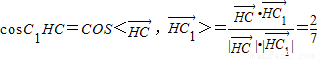 (9分)
(9分)∴
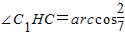 ,
,∴二面角C1-DE-C的大小为ArCCOs
 .(10分)
.(10分)(III)解:在侧棱BB1上不存在点P,使得CP⊥平面C1DE(11分)
证明如下:
假设CP⊥平面C1DE,则必有CP⊥DE.
设P(2,2,a),其中0≤a≤3,
则
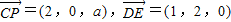 ,
,∵
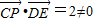 ,这显然与CP⊥DE矛盾.
,这显然与CP⊥DE矛盾.∴假设CP⊥平面C1DE不成立,
即在侧棱BB1上不存在点P,使得CP⊥平面C1DE.(14分)
点评:本题考查直线与平面的存在,二面角的求法等知识,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是