Question

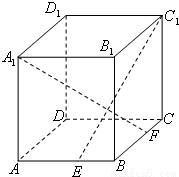
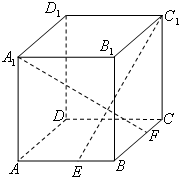如图，ABCD-A₁B₁C₁D₁是棱长为6的正方体，E、F分别是棱AB、BC上的动点，且AE=BF．
（1）求证：A₁F⊥C₁E；
（2）当A₁、E、F、C₁共面时，求：
①D₁到直线C₁E的距离；
②面A₁DE与面C₁DF所成二面角的余弦值．

Answer 1

分析：（1）以D为原点，DA、DC、DD₁所在直线分别为x轴、y轴、z轴建立空间直角坐标系，我们易给出正方体中各个点的坐标，进而求出向量

A1F

，

C1F

坐标，代入向量数量积公式，易得

A1F

•

C1F

=0，即A₁F⊥C₁E；
（2）①在正方体ABCD-A₁B₁C₁D₁中，AB∥C₁D₁，则△BC₁D₁与△EC₁D₁面积相待，故D₁到直线C₁E的距离h满足

C1E×h

2

=

C1D1×BC1

2

，代入即可得到答案；
②我们求出面A₁DE与面C₁DF的法向量，求出两个向量夹角的余弦的绝对值，即可得到答案．

解答：解：（1）以D为原点，DA、DC、DD₁所在直线分别为x轴、y轴、z轴建立空间直角坐标系，
则A₁（6，0，6）、C₁（0，6，6），设AE=m，则E（6，m，0），F（6-m，6，0），
从而

A1F

=(-m ， 6 ， -6)、

C1E

=(6 ， m-6 ， -6)，
∵

A1F

•

C1F

=0，
所以A₁F⊥C₁E（4分）．
（2）①当A₁、E、F、C₁共面时，
因为底面ABCD∥A₁B₁C₁D₁，
所以A₁C₁∥EF，
所以EF∥AC，
从而E、F分别是AB、BC的中点（7分），
设D₁到直线C₁E的距离为h，
在△C₁D₁E中，C1E=

62+62+32

=9，

C1E×h

2

=

C1D1×BC1

2

，
解得h=4

2

（7分）．
②由①得，E（6，3，0）、F（3，6，0），
设平面A₁DE的一个法向量为

n1

=(a ， b ， c)，
依题意

n1 • DE =6a+3b=0 n1 • DA1 =6a+6c=0

，
所以

n1

=(-1 ， 2 ， 1)，
同理平面C₁DF的一个法向量为

n2

=(2 ， -1 ， 1)，
由图知，面A₁DE与面C₁DF所成二面角的余弦值
cosθ=

| n1 • n2 |

| n1 |•| n2 |

=

1

2

点评：本题考查的知识点是向量语言表述线线的垂直、平行关系，点、线、面间的距离计算、用空间向量求平面间的夹角，其中建立空间坐标系，将总是转化为一个向量计算问题是解答本题的关键．