题目内容
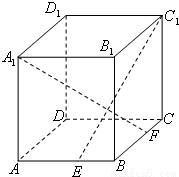
 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是①②
①②
.(把你认为正确的结论都填上)①BD∥平面CB1D1;
②AC1⊥平面CB1D1;
③过点A1与异面直线AD和CB1成90°角的直线有2条.
分析:根据直线和平面平行、直线和平面垂直的判定定理可得判断①②的真假,根据异面直线所成的角可得③不正确,由此得到答案.
解答:解:如图,正方体ABCD-A1B1C1D1 中,
由于BD∥B1D1 ,由直线和平面平行的判定定理可得BD∥平面CB1D1 ,故①正确.
由正方体的性质可得B1D1⊥A1C1,CC1⊥B1D1,故B1D1⊥平面 ACC1A1,故 B1D1⊥AC1.
同理可得 B1C⊥AC1.再根据直线和平面垂直的判定定理可得,AC1⊥平面CB1D1 ,故②正确.
过点A1与异面直线AD成90°角的直线必和BC也垂直
过点A1与直线CB1成90°角的直线必和CB1垂直
则该直线必和平面B1C1CB垂直,满足条件的只有直线A1B1,
故③不正确.
故答案为 ①②
由于BD∥B1D1 ,由直线和平面平行的判定定理可得BD∥平面CB1D1 ,故①正确.
由正方体的性质可得B1D1⊥A1C1,CC1⊥B1D1,故B1D1⊥平面 ACC1A1,故 B1D1⊥AC1.
同理可得 B1C⊥AC1.再根据直线和平面垂直的判定定理可得,AC1⊥平面CB1D1 ,故②正确.
过点A1与异面直线AD成90°角的直线必和BC也垂直
过点A1与直线CB1成90°角的直线必和CB1垂直
则该直线必和平面B1C1CB垂直,满足条件的只有直线A1B1,
故③不正确.
故答案为 ①②
点评:本题主要考查求二面角的大小的方法,异面直线的判定,直线和平面平行、垂直的判定定理的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
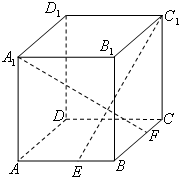 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是