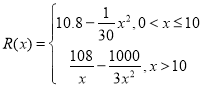题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若对于任意实数![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的范围;
的范围;
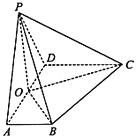
(2)当![]() 时,是否存在实数
时,是否存在实数![]() ,使曲线
,使曲线![]() :
:![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直?若存在,求出
轴垂直?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() ;(2)不存在实数
;(2)不存在实数![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直.
轴垂直.
【解析】
(1)分类![]() 时,恒成立,
时,恒成立,![]() 时,分离参数为
时,分离参数为![]() ,引入新函数
,引入新函数![]() ,利用导数求得函数最值即可;
,利用导数求得函数最值即可;
(2)![]() ,导出导函数
,导出导函数![]() ,问题转化为
,问题转化为![]() 在
在![]() 上有解.再用导数研究
上有解.再用导数研究![]() 的性质可得.
的性质可得.
解:(1)因为当![]() 时,
时,![]() 恒成立,
恒成立,
所以,若![]() ,
,![]() 为任意实数,
为任意实数,![]() 恒成立.
恒成立.
若![]() ,
,![]() 恒成立,
恒成立,
即当![]() 时,
时,![]() ,
,
设![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() 取得最大值.
取得最大值.
![]() ,
,
所以,要使![]() 时,
时,![]() 恒成立,
恒成立,![]() 的取值范围为
的取值范围为![]() .
.
(2)由题意,曲线![]() 为:
为:![]() .
.
令![]() ,
,
所以![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,
,
故![]() 在
在![]() 上为增函数,因此
上为增函数,因此![]() 在区间
在区间![]() 上的最小值
上的最小值![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
所以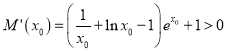 ,
,
曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直等价于方程
轴垂直等价于方程![]() 在
在![]() 上有实数解.
上有实数解.
而![]() ,即方程
,即方程![]() 无实数解.
无实数解.
故不存在实数![]() ,使曲线
,使曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直.
轴垂直.

【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
列联表,并判断能否有95%的把握认为是否生二孩与头胎的男女情况有关;
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)在抽取的200户家庭的样本中,按照分层抽样的方法在生二孩的家庭中抽取了7户,进一步了解情况,在抽取的7户中再随机抽取4户,求抽到的头胎是女孩的家庭户数![]() 的分布列及数学期望.
的分布列及数学期望.
附:
| 0.15 | 0.05 | 0.01 | 0.001 |
| 2.072 | 3.841 | 6.635 | 10.828 |
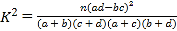 (其中
(其中![]() ).
).
【题目】在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分100分,按照大于或等于80分的为优秀,小于80分的为合格,为了解学生的在该维度的测评结果,在毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表:
优秀 | 合格 | 总计 | |
男生 | 6 | ||
女生 | 18 | ||
合计 | 60 |
已知在该班随机抽取1人测评结果为优秀的概率为![]() .
.
(1)完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
(3)现在如果想了解全校学生在该维度的表现情况,采取简单随机抽样方式在全校学生中抽取少数一部分来分析,请你选择一个合适的抽样方法,并解释理由.
附: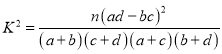
| 0.25 | 0.10 | 0.025 |
| 1.323 | 2.706 | 5.024 |
【题目】某市正在进行创建全国文明城市的复验工作,为了解市民对“创建全国文明城市”的知识知晓程度,某权威调查机构对市民进行随机调查,并对调查结果进行统计,共分为优秀和一般两类,先从结果中随机抽取100份,统计得出如下![]() 列联表:
列联表:
优秀 | 一般 | 总计 | |
男 | 25 | 25 | 50 |
女 | 30 | 20 | 50 |
总计 | 55 | 45 | 100 |
(1)根据上述列联表,是否有![]() 的把握认为“创城知识的知晓程度是否为优秀与性别有关”?
的把握认为“创城知识的知晓程度是否为优秀与性别有关”?
(2)现从调查结果为一般的市民中,按分层抽样的方法从中抽取9人,然后再从这9人中随机抽取3人,求这三位市民中男女都有的概率;
(3)以样本估计总体,视样本频率为概率,从全市市民中随机抽取10人,用![]() 表示这10人中优秀的人数,求随机变量
表示这10人中优秀的人数,求随机变量![]() 的期望和方差.
的期望和方差.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
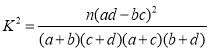 (其中
(其中![]() ).
).
【题目】我市某区2018年房地产价格因“棚户区改造”实行货币化补偿,使房价快速走高,为抑制房价过快上涨,政府从2019年2月开始采用实物补偿方式(以房换房),3月份开始房价得到很好的抑制,房价渐渐回落,以下是2019年2月后该区新建住宅销售均价的数据:
月份 | 3 | 4 | 5 | 6 | 7 |
价格 | 83 | 82 | 80 | 78 | 77 |
(1)研究发现,3月至7月的各月均价![]() (百元/平方米)与月份
(百元/平方米)与月份![]() 之间具有较强的线性相关关系,求价格
之间具有较强的线性相关关系,求价格![]() (百元/平方米)关于月份
(百元/平方米)关于月份![]() 的线性回归方程;
的线性回归方程;
(2)用![]() 表示用(1)中所求的线性回归方程得到的与
表示用(1)中所求的线性回归方程得到的与![]() 对应的销售均价的估计值,3月份至7月份销售均价估计值
对应的销售均价的估计值,3月份至7月份销售均价估计值![]() 与实际相应月份销售均价
与实际相应月份销售均价![]() 差的绝对值记为
差的绝对值记为![]() ,即
,即![]() ,
,![]() .若
.若![]() ,则将销售均价的数据
,则将销售均价的数据称为一个“好数据”,现从5个销售均价数据中任取2个,求抽取的2个数据均是“好数据”的概率.
参考公式:回归方程系数公式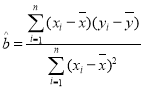 ,
,![]() ;参考数据:
;参考数据:![]() ,
,![]() .
.