题目内容
已知A、B 是抛物线y2=4x上的两点，O是抛物线的顶点，OA⊥OB ．
(1) 求证：直线AB 过定点M(4，0) ；
(2) 设弦AB 的中点为P，求点P 到直线x-y=0的距离的最小值．
(2) 设弦AB 的中点为P，求点P 到直线x-y=0的距离的最小值．
(1)证明：设直线AB方程为x=my+b，A(x1，y1)，B(x2，y1)．
将直线AB方程代入抛物线方程y2=4x，得y2-4my-4b=0，
则y1+y2=4m,y1y2=-4b.
∵OA⊥OB，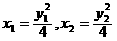
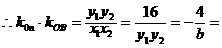-1,b=4.
于是直线AB方程为x=my+4，该直线过定点(4，0).
(2)解：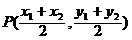
到直线x-y=0的距离
=
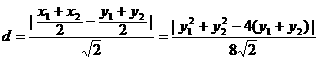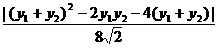
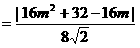
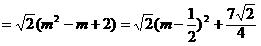
当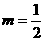
时，d取最小值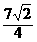
将直线AB方程代入抛物线方程y2=4x，得y2-4my-4b=0，
则y1+y2=4m,y1y2=-4b.
∵OA⊥OB，
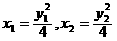
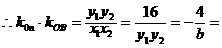-1,b=4.于是直线AB方程为x=my+4，该直线过定点(4，0).
(2)解：
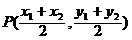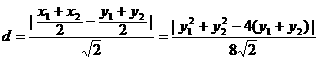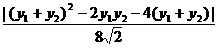
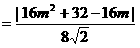
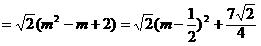
到直线x-y=0的距离=当
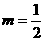时，d取最小值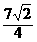
练习册系列答案
相关题目