��Ŀ����
����С������12�֣�ijУ���л���֪ʶ�����������ֳ����;��������֣���������ѡ��ѡһ���һ��ķ�ʽ���У�ÿλѡ�������5��ѡ�����Ļ��ᣬѡ���ۼƴ��3�����3�⼴��ֹ������ı��������3����ֱ�ӽ�����������3��������̭����֪ѡ�ּ״����������δ���ĸ���Ϊ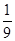 ������֪�ش�ÿ���������ȷ����ͬ�������֮��û��Ӱ�졣����I�����ѡ�ֻش�һ���������ȷ�ʣ�������ѡ�ּɽ�������ĸ��ʣ�������ѡ�ּ��ڳ����д���ĸ���Ϊ
������֪�ش�ÿ���������ȷ����ͬ�������֮��û��Ӱ�졣����I�����ѡ�ֻش�һ���������ȷ�ʣ�������ѡ�ּɽ�������ĸ��ʣ�������ѡ�ּ��ڳ����д���ĸ���Ϊ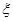 ����д��
����д��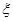 �ķֲ��У�����
�ķֲ��У�����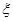 ����ѧ������
����ѧ������
��1��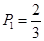 ��2��
��2��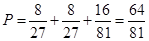 ��3��
��3��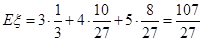
��������
����������⣺��1�����ѡ�ִ��һ���������ȷ��Ϊ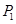 ����
����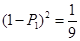
�ʼ�ѡ�ִ��һ���������ȷ��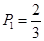 3��
3��
����ѡ�ּ״���3����Ŀ��������ĸ���Ϊ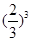 =
=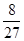 4��
4��
ѡ�ּ״���4����Ŀ��������ĸ���Ϊ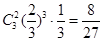 5��
5��
ѡ�ּ״���5����Ŀ��������ĸ���Ϊ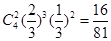 6��
6��
ѡ�ּ��Խ�������ĸ���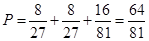 7��
7��
����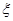 ��ȡ3��4��5����
��ȡ3��4��5����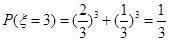 8��
8��
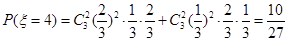 9��
9��
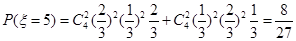 10��
10��
|
|
3 |
4 |
5 |
|
|
|
|
|
��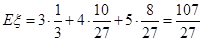 12��
12��
���㣺�����¼��ĸ��ʺͶ���ֲ�������
���������������Ĺؼ�������������¼��ĸ���������������ֵ��ͬʱ�ܽ�϶����ظ�����ĸ��ʹ�ʽ���ֲ��к�����ֵ�����ڻ����⡣