题目内容
已知函数f(x)=x|x-2a|,a∈R.(1)当a=1时,解方程f(x)=0;
(2)当0<a<3时,求函数y=f(x)在区间[0,7]的最大值g(a);
(3)若函数y=f(x)在区间(m,n)上既有最大值又有最小值,请分别求出m,n的取值范围.
【答案】分析:(1)当a=1时,由x|x-2|=0即可求得方程f(x)=0的解;
(2)因为0<a<3,对称轴x=a处于区间[0,7]的偏左部分,g(a)=f(7)=49-14a,由a2=7(7-2a),解得a=7( -1),从而可得答案;
-1),从而可得答案;
(3)当a=0时,f(x)=x|x|,可分析出f(x)在区间(m,n)既没有最大值也没有最小值;当a>0时,由a2=x(x-2a)得x=( +1)a,从而得0≤m<a,2a<n≤(
+1)a,从而得0≤m<a,2a<n≤( +1)a;当a<0时,同理可得(
+1)a;当a<0时,同理可得(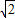 +1)a≤m<2a,a<n≤0.
+1)a≤m<2a,a<n≤0.
解答:解:(1)当a=1时,x|x-2|=0,解得x=0或x=2;…(2分)
(2)当x<2a时,f(x)=x(2a-x)=-(x-a)2+a2;
当x≥2a时,f(x)=x(x-2a)=(x-a)2-a2.
∵0<a<3,对称轴x=a处于区间[0,7]的偏左部分,
由a2=7(7-2a),解得a=7(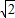 -1)…(6分)
-1)…(6分)
∴g(a)=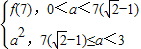 ,
,
即g(a)= …(10分)
…(10分)
(3)当a=0时,f(x)=x|x|,
在区间(m,n)既没有最大值也没有最小值,不符合题意. …(12分)
当a>0时,由a2=x(x-2a)得x=( +1)a,
+1)a,
所以0≤m<a,2a<n≤( +1)a; …(14分)
+1)a; …(14分)
当a<0时,由-a2=x(2a-x)得x=( +1)a,
+1)a,
所以( +1)a≤m<2a,a<n≤0.…(16分)
+1)a≤m<2a,a<n≤0.…(16分)
点评:本题考查带绝对值的函数,突出考查分类讨论思想与方程思想、化归思想的综合应用,考查抽象思维与运算能力,属于难题.
(2)因为0<a<3,对称轴x=a处于区间[0,7]的偏左部分,g(a)=f(7)=49-14a,由a2=7(7-2a),解得a=7(
 -1),从而可得答案;
-1),从而可得答案;(3)当a=0时,f(x)=x|x|,可分析出f(x)在区间(m,n)既没有最大值也没有最小值;当a>0时,由a2=x(x-2a)得x=(
 +1)a,从而得0≤m<a,2a<n≤(
+1)a,从而得0≤m<a,2a<n≤( +1)a;当a<0时,同理可得(
+1)a;当a<0时,同理可得(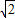 +1)a≤m<2a,a<n≤0.
+1)a≤m<2a,a<n≤0.解答:解:(1)当a=1时,x|x-2|=0,解得x=0或x=2;…(2分)
(2)当x<2a时,f(x)=x(2a-x)=-(x-a)2+a2;
当x≥2a时,f(x)=x(x-2a)=(x-a)2-a2.
∵0<a<3,对称轴x=a处于区间[0,7]的偏左部分,
由a2=7(7-2a),解得a=7(
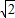 -1)…(6分)
-1)…(6分)∴g(a)=
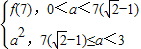 ,
,即g(a)=
 …(10分)
…(10分)(3)当a=0时,f(x)=x|x|,
在区间(m,n)既没有最大值也没有最小值,不符合题意. …(12分)
当a>0时,由a2=x(x-2a)得x=(
 +1)a,
+1)a,所以0≤m<a,2a<n≤(
 +1)a; …(14分)
+1)a; …(14分)当a<0时,由-a2=x(2a-x)得x=(
 +1)a,
+1)a,所以(
 +1)a≤m<2a,a<n≤0.…(16分)
+1)a≤m<2a,a<n≤0.…(16分)点评:本题考查带绝对值的函数,突出考查分类讨论思想与方程思想、化归思想的综合应用,考查抽象思维与运算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|