题目内容
在△ABC中,己知 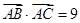 ,sinB= sinCcos
,sinB= sinCcos ,又△ABC的面积为6(Ⅰ)求△ABC的三边长;(Ⅱ)若D为BC边上的一点,且CD=1,求
,又△ABC的面积为6(Ⅰ)求△ABC的三边长;(Ⅱ)若D为BC边上的一点,且CD=1,求 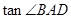 .
.
(Ⅰ) 3,4,5;(Ⅱ) 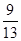
解析试题分析:(Ⅰ)由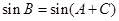 及sinB= sinCcos
及sinB= sinCcos 得sinCcos
得sinCcos =
=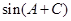 =
=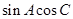
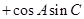 ,所以
,所以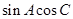 =0,因为
=0,因为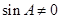 ,所以
,所以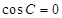 ,所以
,所以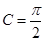 ,由平面向量数量积及三角形面积公式即可求出tanA的值,在Rt△ACB中,tanA=
,由平面向量数量积及三角形面积公式即可求出tanA的值,在Rt△ACB中,tanA= ,求出
,求出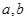 ,代入三角形面积公式求出
,代入三角形面积公式求出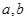 ,利用勾股定理求出c;(Ⅱ)由(Ⅰ)知tan∠BAC=
,利用勾股定理求出c;(Ⅱ)由(Ⅰ)知tan∠BAC=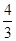 ,由三角函数定义知tan∠DAC=
,由三角函数定义知tan∠DAC= ,利用两角差的正切公式可求得tan∠BAD.
,利用两角差的正切公式可求得tan∠BAD.
试题解析:(Ⅰ)设三边分别为
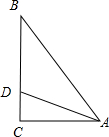
∵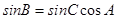 ,∴sin(A+C)=sinCcosA,
,∴sin(A+C)=sinCcosA,
化为sinAcosC+cosAsinC=sinCcosA,
∴sinAcosC=0,可得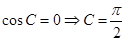
又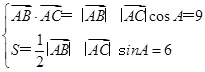
两式相除可得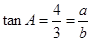
令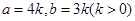
则
 三边长分别为3,4,5, (8分)
三边长分别为3,4,5, (8分)
(Ⅱ)由(Ⅰ)知tan∠BAC=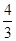 ,由三角函数定义知tan∠DAC=
,由三角函数定义知tan∠DAC= ,
,
所以tan =tan(∠BAC-∠DAC)=
=tan(∠BAC-∠DAC)=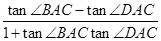 =
=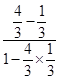 =
=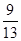 (12分)
(12分)
考点:三角变换,平面向量数量积,三角形面积公式,运算求解能力

练习册系列答案
相关题目
 ,
, ,
, 、
、 均为锐角,则
均为锐角,则 等于 .
等于 .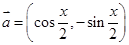 ,
, ,
,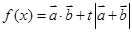 ,
,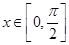 .
.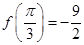 ,求函数
,求函数 的值域;
的值域; 的方程
的方程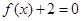 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.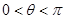 ,
,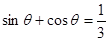 ,求
,求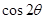 的值;
的值;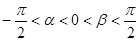 ,
,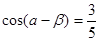 ,
, ,求
,求 的值.
的值. .
.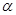 为第三象限角,
为第三象限角,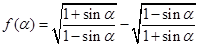 .
.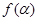 ;
;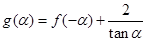 ,求函数
,求函数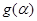 的最小值,并求取最小值时的
的最小值,并求取最小值时的 为第三象限的角,
为第三象限的角,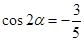 ,则
,则 .
. ;
;
 ;
; .
.  都有意义,你从这三个恒等式中猜想得到的一个结论为 ▲
都有意义,你从这三个恒等式中猜想得到的一个结论为 ▲  的最大值y= ,当取得这个最大值时自变量x的取值的集合是 .
的最大值y= ,当取得这个最大值时自变量x的取值的集合是 .