题目内容
(本题满分13分)已知函数f(x)=cos(-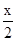 )+cos(
)+cos(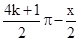 ),k∈Z,x∈R.
),k∈Z,x∈R.
(1)求f(x)的最小正周期;
(2)求f(x)在[0,π)上的减区间;
(3)若f(α)=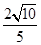 ,α∈(0,
,α∈(0,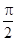 ),求tan(2α+
),求tan(2α+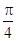 )的值.
)的值.
【答案】
(1) 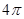 ;(2) [
;(2) [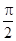 ,π) ;(3)
,π) ;(3)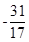 。
。
【解析】。
试题分析:(1)f(x)=cos(-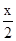 )+cos(
)+cos(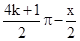 )
)
=cos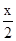 +cos(2kπ+
+cos(2kπ+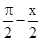 )
)
=sin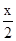 +cos
+cos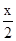 =
=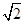 sin(
sin(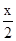 +
+ ), 2分
), 2分
所以,f(x)的最小正周期T=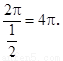 4分
4分
(2)由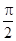 +2kπ≤
+2kπ≤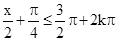 ,k∈Z
,k∈Z
得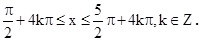
令k=0,得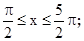
令k=-1,得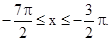 6分
6分
又x∈[0,π),∴f(x)在[0,π)上的减区间是[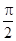 ,π). 8分
,π). 8分
(3)由f(α)=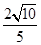 ,得
,得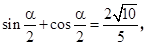
∴1+sinα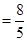 ,∴sinα=
,∴sinα=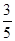 ,
,
又α∈(0,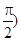 ,∴cosα=
,∴cosα=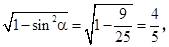 10分
10分
∴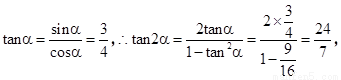
∴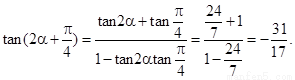 13分
13分
考点:同名的诱导公式;异名的诱导公式;周期公式;和差公式;同角三角函数关系式;三角函数的性质。
点评:函数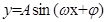 的周期公式为:
的周期公式为: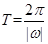 ;函数
;函数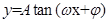 的周期公式为:
的周期公式为: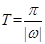 。注意两个函数周期公式的区别。
。注意两个函数周期公式的区别。

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.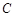 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.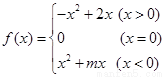 为奇函数;
为奇函数;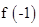 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆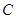 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.