题目内容
(本题满分13分)已知函数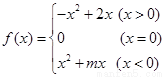 为奇函数;
为奇函数;
(1)求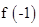 以及m的值;
以及m的值;
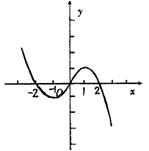
(2)在给出的直角坐标系中画出 的图象;
的图象;

(3)若函数 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
【答案】
(1) m=2.
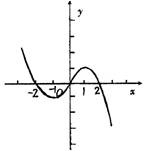
(2)y=f(x)的图象如图所示 .
(3)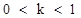 。
。
【解析】
试题分析:(1)根据f(x)为奇函数可知f(-1)=-f(1)从而可建立关于m的方程求出m值.
(2)由于分段函数的对应关系不同,所以要分段画其图像.再画图像时要注意函数关于原点对称.
(3)结合图像可知g(x)由三个零点,也就是方程f(x)=2k-1有三个不同的实数根,即直线y=2k-1与y=f(x)的图像有三个公共点,然后数形结合求解即可.
(1) f(1)=1,f(-1)= -f(1)=-1,…………………2分
当x<0时,-x>0,f(x)= -(x)2+2(-x)=-x2-2x,又f(x)为奇函数,f(x)=-f(-x)=x2+2x,
所以m=2. …………………4分
(2)y=f(x)的图象如图所示 . …………………8分
(3)图象知:若函数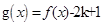 有三个零点,则
有三个零点,则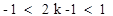 ……………12分,
……………12分,
即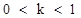 ………………13分
………………13分
考点: 函数的奇偶性,分段函数的图像,函数的零点.
点评:函数的零点与方程的根的关系.

练习册系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.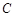 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆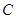 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.