��Ŀ����
1�� (��������12��)
�Ŵ�ӡ�������Ž������ڵ�ɮ�����������һ�ֱ���Ϊ�����ڱ������⡱����Ϸ�����淨���£���ͼ������n�� ����Բ������뾶��С��������£�С����������A���ϣ���Ҫ������A���ϵ��̻���C���ϣ�Ҫ��ÿ��ֻ�ܰᶯһ���������κ�ʱ����������������С�����棬�ٶ�����������A��B��C�ɹ�ʹ�ã�
����Բ������뾶��С��������£�С����������A���ϣ���Ҫ������A���ϵ��̻���C���ϣ�Ҫ��ÿ��ֻ�ܰᶯһ���������κ�ʱ����������������С�����棬�ٶ�����������A��B��C�ɹ�ʹ�ã�

����an��ʾ��n��Բ��ȫ����A�����Ƶ�C������������Ҫ�ƶ��Ĵ������ش��������⣺
(1) �a1��a2��a3�������an��
(2) �� �����
����� ��
�� ����
����
������ ��ʾ���еĻ�
��ʾ���еĻ� �ĺͣ�
�ĺͣ�
(3) ֤����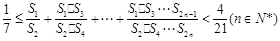 ��
��
���𰸡�
��1��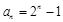 ��2��
��2��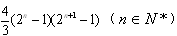 ��3����
��3����
��������(1) 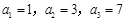
��ʵ�ϣ�Ҫ��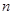 ��Բ��ȫ��ת�Ƶ�C���ϣ�ֻ���Ƚ�����
��Բ��ȫ��ת�Ƶ�C���ϣ�ֻ���Ƚ�����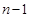 ��Բ��ת�Ƶ�B���ϣ���Ҫ
��Բ��ת�Ƶ�B���ϣ���Ҫ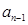 ��ת�ƣ�Ȼ�������Ǹ�Բ��ת�Ƶ�C���ϣ���Ҫһ��ת�ƣ��ٽ�
��ת�ƣ�Ȼ�������Ǹ�Բ��ת�Ƶ�C���ϣ���Ҫһ��ת�ƣ��ٽ�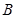 ���ϵ�
���ϵ�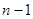 ��Բ��ת�Ƶ�C���ϣ���Ҫ
��Բ��ת�Ƶ�C���ϣ���Ҫ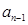 ��ת�ƣ�������
��ת�ƣ�������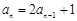
��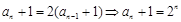 ������
������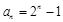
(2) 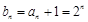
��
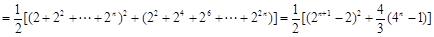
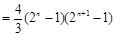 ��
��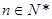 ��
��
(3) ��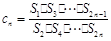 ����
����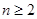 ʱ
ʱ
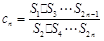
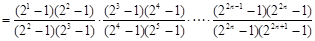
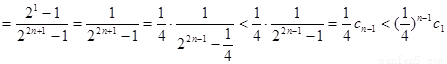
��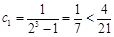 �����Զ�һ��
�����Զ�һ��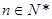 �У�
�У�
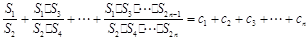
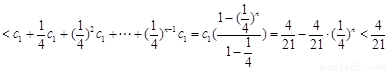
������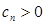 ����������Զ�һ��
����������Զ�һ��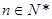 ��
��
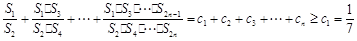
����������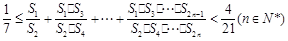

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ