题目内容
10.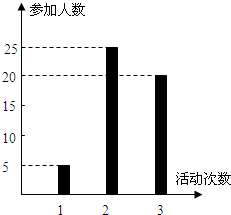 按照新课程的要求,高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).该校高2010级一班50名学生在上学期参加活动的次数统计如图所示.
按照新课程的要求,高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).该校高2010级一班50名学生在上学期参加活动的次数统计如图所示.(1)求该班学生参加活动的人均次数$\overline x$;
(2)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率P0.
(3)从该班中任选两名学生,用ξ表示这两人参加活动次数之差的绝对值,求随机变量ξ的分布列及数学期望Eξ.
分析 (1)根据图形能够知道参加活动1次、2次和3次的学生人数,即可求出该班学生参加活动的人均次数$\overline x$;
(2)“参加活动次数恰好相等”的事件有C52+C252+C202,任选两名学生有C502,可得他们参加活动次数恰好相等的概率P0.
(3)由题意该班中任选两名学生的情况有“这两人中一人参加1次活动,另一人参加2次活动”,“这两人中一人参加2次活动,另一人参加3次活动”,“这两人中一人参加1次活动,另一人参加3次活动”,ξ的取值有0,1,2,求出其概率,进而可以求出数学期望Eξ.
解答 解:由图可知,参加活动1次、2次和3次的学生人数分别为5、25和20.
(1)该班学生参加活动的人均次数为$\overline x$=$\frac{1×5+2×25+3×20}{50}=\frac{115}{50}=\frac{23}{10}$.
(2)从该班中任选两名学生,他们参加活动次数恰好相等的概率为${P_0}=\frac{{C_5^2+C_{25}^2+C_{20}^2}}{{C_{50}^2}}=\frac{20}{49}$.
(3)从该班中任选两名学生,记“这两人中一人参加1次活动,另一人参加2次活动”为事件A,“这两人中一人参加2次活动,另一人参加3次活动”为事件B,“这两人中一人参加1次活动,另一人参加3次活动”为事件C.易知$P(ξ=1)=P(A)+P(B)=\frac{{C_5^1C_{25}^1}}{{C_{50}^2}}+\frac{{C_{25}^1C_{20}^1}}{{C_{50}^2}}=\frac{25}{49}$;
ξ的分布列:
| ξ | 0 | 1 | 2 |
| P | $\frac{20}{49}$ | $\frac{25}{49}$ | $\frac{4}{49}$ |
点评 本题考查概率的计算,考查随机变量ξ的分布列及数学期望Eξ,考查学生的计算能力,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
18.从1,2,3,4,5这5个数字中,不放回地任取两数,则两数都是奇数的概率是( )
| A. | $\frac{9}{25}$ | B. | $\frac{4}{25}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
5.数列$\left\{{tan\frac{n}{9}π•tan\frac{n+1}{9}π}\right\}$的前n项和记为Sn,则S2015=( )
| A. | -2016 | B. | -2015 | C. | -2014 | D. | -1007 |
19.从某企业的某种产品中抽取n件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
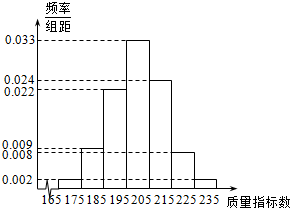
其中第二小组的频数为36,则n为( )

其中第二小组的频数为36,则n为( )
| A. | 200 | B. | 400 | C. | 2000 | D. | 4000 |
20.执行如图所示的程序框图若输出的n=9,则输入的整数p的最小值是( )
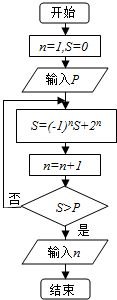

| A. | 50 | B. | 77 | C. | 78 | D. | 306 |