题目内容
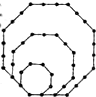 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是341
341
.分析:各个正八边形上的珠子分别有8,2×8,3×8,…10×8 个,把它们相加,再减去多计算的珠子数3×9+2×8+2×7+2×6+…+2×1,即得所求.
解答:解:边长为1,2,3…10 的正八边形叠放在一起,则各个正八边形上的珠子分别有8,2×8,3×8,…10×8 个,
其中,有3个珠子被重复计算了10次,有2个珠子被重复计算了9次,有2个珠子被重复计算了8次,有2个珠子被重复计算了7次,有2个珠子被重复计算了6次,…
有2个珠子被重复计算了2次,
故不同的珠子个数为( 8+2×8+3×8+…+10×8 )-[3×9+2×8+2×7+2×6+…+2×1]=440-(27+2×
)=341,
故答案为 341.
其中,有3个珠子被重复计算了10次,有2个珠子被重复计算了9次,有2个珠子被重复计算了8次,有2个珠子被重复计算了7次,有2个珠子被重复计算了6次,…
有2个珠子被重复计算了2次,
故不同的珠子个数为( 8+2×8+3×8+…+10×8 )-[3×9+2×8+2×7+2×6+…+2×1]=440-(27+2×
| 8×9 |
| 2 |
故答案为 341.
点评:本题主要考查归纳推理,由几个特殊的例子,分析其结构特征,总结出一般规律,等差数列的求和公式,属于基础题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目