题目内容
(本题满分14分)在直角坐标系xOy中,椭圆C1: 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且 .
.
(Ⅰ)求C1的方程;
(Ⅱ)平面上的点N满足 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若 ·
· =0,求直线l的方程.
=0,求直线l的方程.
【答案】
解:(Ⅰ)由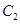 :
: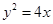 知
知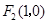 .设
.设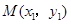 ,
,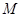 在
在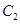 上,因为
上,因为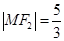 ,所以
,所以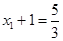 ,得
,得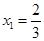 ,
,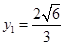 .M在
.M在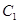 上,且椭圆
上,且椭圆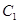 的半焦距
的半焦距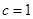 ,于是
,于是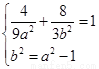 ,消去
,消去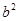 并整理得
并整理得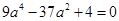 ,解得
,解得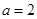 (
(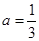 不合题意,舍去).故椭圆
不合题意,舍去).故椭圆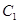 的方程为
的方程为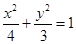 .(6分)
.(6分)
(Ⅱ)由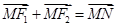 知四边形
知四边形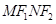 是平行四边形,其中心为坐标原点
是平行四边形,其中心为坐标原点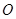 ,
,
因为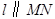 ,所以
,所以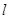 与
与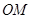 的斜率相同,故
的斜率相同,故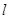 的斜率
的斜率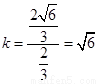 .
.
设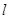 的方程为
的方程为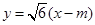 .由
.由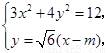 消去
消去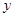 并化简得
并化简得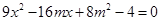 .
.
设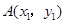 ,
,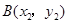 ,
,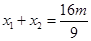 ,
,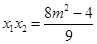 .因为
.因为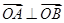 ,所以
,所以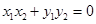 .
.
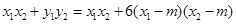
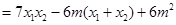
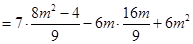
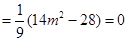 .所以
.所以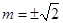 .
.
此时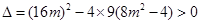 ,
,
故所求直线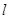 的方程为
的方程为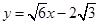 ,或
,或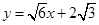 .(14分)
.(14分)
【解析】略

练习册系列答案
相关题目
 中,已知圆
中,已知圆 ,
, .
.
 的直线
的直线 被圆
被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线 是以1为半径,圆心在圆
是以1为半径,圆心在圆 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆 分别作圆
分别作圆 的两条切线
的两条切线 ,切点为
,切点为 ,求
,求 的取值范围 ;
的取值范围 ; 同时平分圆
同时平分圆 的周长、圆
的周长、圆 中,角
中,角 、
、 、
、 所对应的边分别为
所对应的边分别为 、
、 、
、 ,且满足
,且满足
 ,求实数
,求实数 的值。
的值。 ,求
,求 的值.
的值. 的正方体
的正方体 中,
中, 是线段
是线段 的中点,底面ABCD的中心是F.
的中点,底面ABCD的中心是F. ^
^ ;
;  ;
; 的体积。
的体积。