题目内容
10.已知正项数列{an}的前n项和Sn,满足Sn2-(n2+n-1)Sn-(n2+n)=0.(1)求数列{an}的通项公式;
(2)记bn=$\frac{2}{{a}_{n}}$,数列{bn}的前n项和为Tn,证明:当k>7且k∈N时,对任意n∈N,都有Tnk-1-Tn-1>$\frac{3}{2}$.
分析 (1)对已知的式子因式分解,结合条件可得Sn=n2+n,由Sn与an的关系式求出an;
(2)由(1)化简bn=$\frac{2}{{a}_{n}}$,由数列前n项和的定义表示出Tnk-1-Tn-1,由倒序相加法和基本不等式进行放缩,化简后再进行恰当的放缩,由数列函数的特性证明结论成立.
解答 解:(1)由题意得,Sn2-(n2+n-1)Sn-(n2+n)=0,
则(Sn+1)[Sn-(n2+n)]=0,
因为数列{an}的各项是正项,所以Sn=n2+n,
当n=1时,a1=S1=1+1=2,
当n≥2时,an=Sn-Sn-1=n2+n-[(n-1)2+(n-1)]=2n,
经验证n=1时也适合上式,所以an=2n;
证明:(2)由(1)得,bn=$\frac{2}{{a}_{n}}$=$\frac{2}{2n}$=$\frac{1}{n}$,
所以k>7时,S=Tnk-1-Tn-1=$\frac{1}{n}+\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{nk-1}$,
则2S=$(\frac{1}{n}+\frac{1}{nk-1})+(\frac{1}{n+1}+\frac{1}{nk-2})+(\frac{1}{n+2}+\frac{1}{nk-3})+…+(\frac{1}{nk-1}$$+\frac{1}{n})$,
当x>0,y>0时,$x+y≥2\sqrt{xy}$、$\frac{1}{x}+\frac{1}{y}≥2\sqrt{\frac{1}{xy}}$,当且仅当x=y时等号成立.
∴$(x+y)(\frac{1}{x}+\frac{1}{y})≥2\sqrt{\frac{1}{xy}}•2\sqrt{xy}$=4,则$\frac{1}{x}+\frac{1}{y}≥\frac{4}{x+y}$当且仅当x=y时等号成立.
∵上述(1)式中,k>7,n>0,n+1,n+2,…,nk-1全为正,
∴2S>$\frac{4}{n+nk-1}+\frac{4}{n+1+nk-2}+\frac{4}{n+2+nk-3}+$…+$\frac{1}{nk-1+n}$
=$\frac{4(nk-n)}{n+nk-1}$=$\frac{4n(k-1)}{n+nk-1}$,
∴S>$\frac{2n(k-1)}{n+nk-1}$=$\frac{2(k-1)}{1+k-\frac{1}{n}}$>$\frac{2(k-1)}{1+k}$=2(1-$\frac{2}{k+1}$)>2(1-$\frac{2}{7+1}$)=$\frac{3}{2}$,
综上可得,当k>7且k∈N时,对任意n∈N,都有Tnk-1-Tn-1>$\frac{3}{2}$.
点评 本题考查数列的递推公式的化简、变形,数列的Sn与an的关系式求通项公式,基本不等式等,考查利用放缩法证明不等式,倒序相加法求和,化归与转化的数学思想,培养学生的抽象概括能力、推理论证能力、运算求解能力和创新意识.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | 6$+2\sqrt{2}$ | B. | 6$+2\sqrt{3}$ | C. | 6$+\sqrt{2}$ | D. | 6$+\sqrt{3}$ |
 如图所示,设F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,A、B分别为其左顶点与上顶点,椭圆的离心率e=$\frac{1}{2}$,原点到过点A、B的直线的距离为$\frac{{2\sqrt{21}}}{7}$.
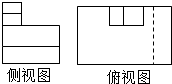
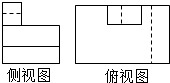
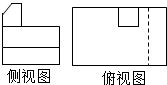
如图所示,设F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,A、B分别为其左顶点与上顶点,椭圆的离心率e=$\frac{1}{2}$,原点到过点A、B的直线的距离为$\frac{{2\sqrt{21}}}{7}$. 如图所示是一位同学画的一个实物的三视图,老师判断正视图是正确的,其他两个视图有错误,则正确的侧视图和俯视图是( )
如图所示是一位同学画的一个实物的三视图,老师判断正视图是正确的,其他两个视图有错误,则正确的侧视图和俯视图是( )