题目内容
已知 在区间
在区间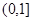 上单调递减,则实数
上单调递减,则实数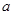 的取值范围是
的取值范围是 .
.
 在区间
在区间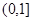 上单调递减,则实数
上单调递减,则实数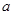 的取值范围是
的取值范围是 .
. 或
或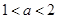
试题分析:
 时,
时, ,
,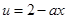 是减函数,
是减函数,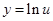 是增函数,同时须
是增函数,同时须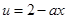 在
在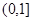 满足大于0,即
满足大于0,即 ,所以,
,所以,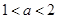 ;
;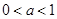 时,
时,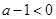 ,
,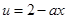 是减函数,
是减函数,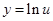 是增函数,函数
是增函数,函数 为增函数;
为增函数; 时,
时,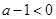 ,
,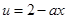 是增函数,
是增函数,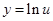 是增函数,函数
是增函数,函数 为减函数,同时,
为减函数,同时,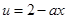 在
在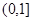 满足大于0,所以,
满足大于0,所以, ;
;综上知,实数
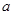 的取值范围是
的取值范围是 或
或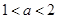 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
 在区间
在区间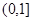 上单调递减,则实数
上单调递减,则实数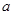 的取值范围是
的取值范围是 .
. 或
或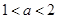
 时,
时, ,
,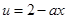 是减函数,
是减函数,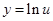 是增函数,同时须
是增函数,同时须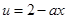 在
在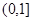 满足大于0,即
满足大于0,即 ,所以,
,所以,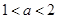 ;
;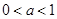 时,
时,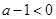 ,
,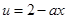 是减函数,
是减函数,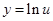 是增函数,函数
是增函数,函数 为增函数;
为增函数; 时,
时,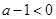 ,
,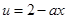 是增函数,
是增函数,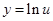 是增函数,函数
是增函数,函数 为减函数,同时,
为减函数,同时,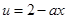 在
在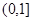 满足大于0,所以,
满足大于0,所以, ;
;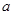 的取值范围是
的取值范围是 或
或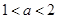 .
.
 阅读快车系列答案
阅读快车系列答案