题目内容
若等差数列{an}与等比数列{bn}的首项是相等的正数,且它们的第2n+1项也相等,则有( )
| A、an+1<bn+1 | B、an+1≤bn+1 | C、an+1≥bn+1 | D、an+1>bn+1 |
分析:先利用等差中项和等比中项的定义把an+1和bn+1表示出来,在对其作差利用基本不等式得结论.
解答:解:因为等差数列{an}和等比数列{bn}各项都是正数,且a1=b1,a2n+1=b2n+1,
所以an+1-bn+1=
-
=
=
≥0.
即 an+1≥bn+1.
故选C.
所以an+1-bn+1=
| a1+a2n+1 |
| 2 |
| b1•b2n+1 |
a1+a2n+1-2
| ||
| 2 |
(
| ||||
| 2 |
即 an+1≥bn+1.
故选C.
点评:本题主要考查基本不等式及等差中项:x,A,y成等差数列?2A=x+y,等比中项:x、G、y成等比数列⇒G2=xy,或G=±xy.

练习册系列答案
相关题目
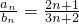 ,{an}的前n项和记为Sn,{bn}的前n项和记为Tn,则
,{an}的前n项和记为Sn,{bn}的前n项和记为Tn,则 =________.
=________.