Question

已知a、b是非零向量且满足(a-2b)⊥a,(b-2a)⊥b,则a与b的夹角是(　　)

A.                            B.                            C.                         D.

Answer 1

思路分析：设a与b的夹角是α,∵(a－2b)⊥a,

∴(a－2b)·a=0,即|a|²－2a·b=0.                                                            ①

又∵(b－2a)⊥b,∴(b－2a)·b=0,

即|b|²－2a·b=0.                                                                                   ②

由①②,知|a|=|b|,a·b=|a|²=|b|².

∴cosα=.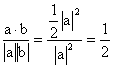

∴a与b的夹角为.

答案：B