题目内容
【题目】在平面直角坐标系![]() 中,点
中,点![]() 点关于原点
点关于原点![]() 对称的点为
对称的点为![]() 二次函数
二次函数![]() 的图像经过点
的图像经过点![]() 和点
和点![]() 回答以下问题:
回答以下问题:
(1)用![]() 表示
表示![]() 和
和![]() 的图像的顶点的纵坐标;
的图像的顶点的纵坐标;
(2)证明:若二次函数![]() 的图像上的点
的图像上的点![]() 满足
满足![]() ,则向量
,则向量![]() 与
与![]() 的数量积大于
的数量积大于![]() .
.
(3)当变![]() 化时,求
化时,求![]() 中二次函数顶点纵坐标
中二次函数顶点纵坐标![]() 的最大值,并求出此时
的最大值,并求出此时![]() 的值.
的值.
【答案】(1)![]() (2)见详解(3)
(2)见详解(3)![]() ,
,![]()
【解析】
(1)根据A点坐标得出B点坐标,将A,B坐标代入![]() ,解得
,解得![]() 代入
代入![]() ,配方即得;(2)用坐标表示出
,配方即得;(2)用坐标表示出![]() ,根据
,根据![]() 和函数单调性,即得;(3)由
和函数单调性,即得;(3)由![]() 和基本不等式可得。
和基本不等式可得。
(1)由题得,点![]() ,且有
,且有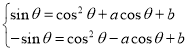 ,整理可得
,整理可得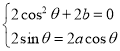 ,即
,即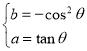 ,则
,则![]() ,整理得
,整理得![]() ,顶点坐标为
,顶点坐标为![]() ,则顶点的纵坐标为
,则顶点的纵坐标为![]() .
.
(2)证明:由题得![]() ,
,
![]() ,设
,设![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() 为单调递增函数,
为单调递增函数,![]() ,又
,又![]() ,故
,故![]() ,即
,即![]() 得证.
得证.
(3)由(1)得顶点纵坐标为![]() ,又
,又![]() ,且
,且![]() ,则
,则![]() ,
,![]() ,等号成立时
,等号成立时![]() ,则
,则![]() ,故
,故![]() 中二次函数顶点纵坐标
中二次函数顶点纵坐标![]() 的最大值为
的最大值为![]() ,此时
,此时![]() .
.

【题目】随着电商的快速发展,快递业突飞猛进,到目前,中国拥有世界上最大的快递市场.某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除
的包裹,除![]() 收费10元之外,每超过
收费10元之外,每超过![]() (不足
(不足![]() ,按
,按![]() 计算)需再收5元.
计算)需再收5元.
该公司将最近承揽的100件包裹的重量统计如下:
包裹重量(单位: | 1 | 2 | 3 | 4 | 5 |
包裹件数 | 43 | 30 | 15 | 8 | 4 |
公司对近60天,每天揽件数量统计如下表:
包裹件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
包裹件数(近似处理) | 50 | 150 | 250 | 350 | 450 |
天数 | 6 | 6 | 30 | 12 | 6 |
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来5天内恰有2天揽件数在101~300之间的概率;
(2)①估计该公司对每件包裹收取的快递费的平均值;
②根据以往的经验,公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员3人,每人每件揽件不超过150件,日工资100元.公司正在考虑是否将前台工作人员裁减1人,试计算裁员前后公司每日利润的数学期望,若你是公司老总,是否进行裁减工作人员1人?
【题目】迈入2018年后,直播答题突然就火了.在1月6号的一场活动中,最终仅有23人平分100万,这23人可以说是“学霸”级的大神.随着直播答题的发展,平台“烧钱大战”模式的可持续性受到了质疑,某网站随机选取1000名网民进行了调查,得到的数据如下表:
男 | 女 | |
认为直播答题模式可持续 | 360 | 280 |
认为直播答题模式不可持续 | 240 | 120 |
(1)根据表格中的数据,能否在犯错误不超过![]() 的前提下,认为对直播答题模式的态度与性别有关系?
的前提下,认为对直播答题模式的态度与性别有关系?
(2)已知在参与调查的1000人中,有20%曾参加答题游戏瓜分过奖金,而男性被调查者有15%曾参加游戏瓜分过奖金,求女性被调查者参与游戏瓜分过奖金的概率.
参考公式: ![]() .
.
临界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |