题目内容
【题目】已知
为坐标原点，点
，
，
，动点
满足
，点
为线段
的中点，抛物线
：
上点
的纵坐标为
，
.
（1）求动点的轨迹曲线
的标准方程及抛物线的标准方程；
（2）若抛物线的准线上一点
满足
，试判断
是否为定值，若是，求这个定值；若不是，请说明理由.
【答案】（1）曲线
的标准方程为
.抛物线
的标准方程为
.（2）见解析
【解析】
（1）由题知|PF1|+|PF2|
2
|F1F2|，判断动点P的轨迹W是椭圆，写出椭圆的标准方程，根据平面向量数量积运算和点A在抛物线上求出抛物线C的标准方程；（2）设出点P的坐标，再表示出点N和Q的坐标，根据题意求出
的值，即可判断结果是否成立．
（1）由题知
，
，
所以
，
因此动点
的轨迹是以
，
为焦点的椭圆，
又知
，
，
所以曲线的标准方程为.
又由题知
，
所以
，
所以
，
又因为点
在抛物线上，所以
，
所以抛物线的标准方程为.
（2）设
，
，
由题知
，所以
，即
，
所以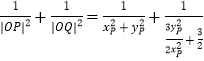
，
又因为
，
，
所以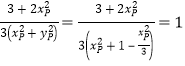
，
所以为定值，且定值为1.
练习册系列答案
相关题目
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷（guǐ）影长的记录中，冬至和夏至的晷影长是实测得到的，其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录，其中
寸表示115寸
分（1寸=10分）.
节气 | 冬至 | 小寒（大雪） | 大寒（小雪） | 立春（立冬） | 雨水（霜降） |
晷影长（寸） | 135 |
|
|
|
|
节气 | 惊蛰（寒露） | 春分（秋分） | 清明（白露） | 谷雨（处暑） | 立夏（立秋） |
晷影长（寸） |
| 75.5 |
|
|
|
节气 | 小满（大暑） | 芒种（小暑） | 夏至 | ||
晷影长（寸） |
|
| 16.0 |
已知《易经》中记录的冬至晷影长为130.0寸，春分晷影长为72.4寸，那么《易经》中所记录的夏至的晷影长应为（ ）
A. 14.8寸B. 15.8寸C. 16.0寸D. 18.4寸
