题目内容
在平面直角坐标系中，已知两点A（2，5），B（0，1），若点C满足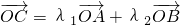
（O为坐标原点），其中λ1、λ2∈R，且λ1+λ2=1，则点C的轨迹方程为________．
2x-y+1=0
分析：由点C满足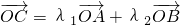，其中λ1、λ2∈R，且λ1+λ2=1，知点C在直线AB上，故求出直线AB的方程即求出点C的轨迹方程．
解答：C点满足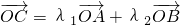且λ1、λ2∈R，且λ1+λ2=1，
∴A、B、C三点共线．
∴C点的轨迹是直线AB
又A（2，5），B（0，1），
∴直线AB的方程为：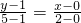
整理得2x-y+1=0
故C点的轨迹方程为2x-y+1=0
故答案为：2x-y+1=0．
点评：考查平面向量中三点共线的充要条件及知两点求直线的方程，是向量与解析几何综合运用的一道比较基本的题，难度较小，知识性较强．
分析：由点C满足
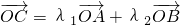，其中λ1、λ2∈R，且λ1+λ2=1，知点C在直线AB上，故求出直线AB的方程即求出点C的轨迹方程．解答：C点满足
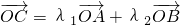且λ1、λ2∈R，且λ1+λ2=1，∴A、B、C三点共线．
∴C点的轨迹是直线AB
又A（2，5），B（0，1），
∴直线AB的方程为：
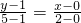整理得2x-y+1=0故C点的轨迹方程为2x-y+1=0
故答案为：2x-y+1=0．
点评：考查平面向量中三点共线的充要条件及知两点求直线的方程，是向量与解析几何综合运用的一道比较基本的题，难度较小，知识性较强．
练习册系列答案
相关题目