题目内容
在平面直角坐标系中,以点(1,0)为圆心,r为半径作圆,依次与抛物线y2=x交于A、B、C、D四点,若AC与BD的交点F恰好为抛物线的焦点,则r= .
分析:根据抛物线方程可求得焦点坐标,设过F的直线方程,与抛物线方程联立,整理后,设A(x1,y1),C(x2,y2)根据韦达定理可求得x1x2的值,又根据圆的方程,可知x1x2=1-r2代入答案可得.
解答: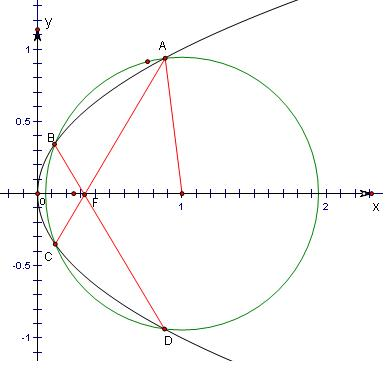 解:易知焦点F坐标(
解:易知焦点F坐标(
,0),
设过F点直线方程为y=k(x-
)
代入抛物线方程,得 k2(x-
)2=4x.
化简后为:k2x2-(
k2+)x+
k2=0.
设A(x1,y1),C(x2,y2)
则有x1x2=
,
又以点(1,0)为圆心,r为半径圆的方程为(x-1)2+y2-r2=0代入抛物线方程,得:x2-x+1-r2=0.
则有x1x2=1-r2,
∴1-r2=
,∴r=
,
故答案为:
.
 解:易知焦点F坐标(
解:易知焦点F坐标(| 1 |
| 4 |
设过F点直线方程为y=k(x-
| 1 |
| 4 |
代入抛物线方程,得 k2(x-
| 1 |
| 4 |
化简后为:k2x2-(
| 1 |
| 2 |
| 1 |
| 16 |
设A(x1,y1),C(x2,y2)
则有x1x2=
| 1 |
| 16 |
又以点(1,0)为圆心,r为半径圆的方程为(x-1)2+y2-r2=0代入抛物线方程,得:x2-x+1-r2=0.
则有x1x2=1-r2,
∴1-r2=
| 1 |
| 16 |
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题主要考查抛物线的应用和抛物线定义.对于过抛物线焦点的直线与抛物线关系,常用方程思想来解决.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目