题目内容
6.已知$\overrightarrow{a}$,$\overrightarrow{b}$不共线,且$\overrightarrow{c}$=λ1$\overrightarrow{a}$+λ2$\overrightarrow{b}$(λ1,λ2∈R),若$\overrightarrow{c}$∥$\overrightarrow{b}$,则λ1=0.分析 $\overrightarrow{c}$∥$\overrightarrow{b}$,可得存在实数k使得$\overrightarrow{c}=k\overrightarrow{b}$,可得${λ}_{1}\overrightarrow{a}+({λ}_{2}-k)\overrightarrow{b}$=$\overrightarrow{0}$,利用$\overrightarrow{a}$,$\overrightarrow{b}$不共线,即可得出.
解答 解:∵$\overrightarrow{c}$∥$\overrightarrow{b}$,
∴存在实数k使得$\overrightarrow{c}=k\overrightarrow{b}$,
∴$\overrightarrow{c}$=λ1$\overrightarrow{a}$+λ2$\overrightarrow{b}$=$k\overrightarrow{b}$,
化为${λ}_{1}\overrightarrow{a}+({λ}_{2}-k)\overrightarrow{b}$=$\overrightarrow{0}$,
∵$\overrightarrow{a}$,$\overrightarrow{b}$不共线,
∴λ1=λ2-k=0,
解得λ1=0.
故答案为:0.
点评 本题考查了向量共线定理与向量共面基本定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.设a>-b,则下列不等式中,成立的是( )
| A. | a(a+b)2<-b(a+b)2 | B. | a(a+b)2>-b(a+b)2 | C. | a(a+b)2≤-b(a+b)2 | D. | a(a+b)2≥-b(a+b)2 |
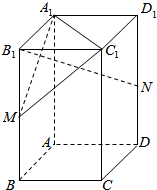 正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别为BB1,DD1的中点.
正四棱柱ABCD-A1B1C1D1中,AB=a,AA1=2a,M,N分别为BB1,DD1的中点.